1382.将二叉搜索树变平衡：分治——求得所有节点再重新建树

【LetMeFly】1382.将二叉搜索树变平衡：分治——求得所有节点再重新建树

力扣题目链接：https://leetcode.cn/problems/balance-a-binary-search-tree/

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

 

示例 1：

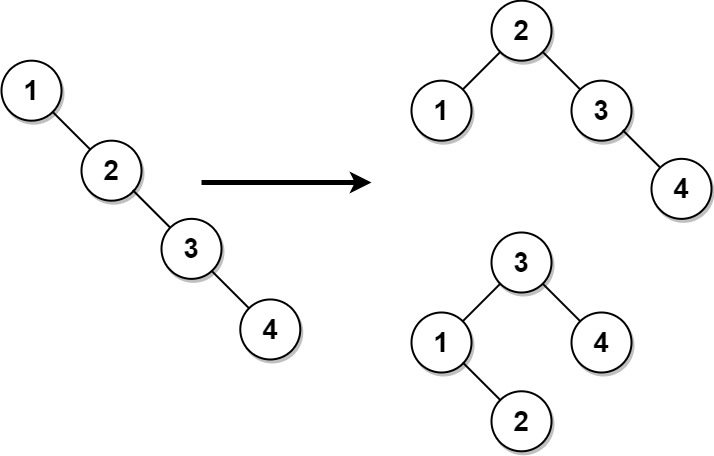
输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

示例 2：

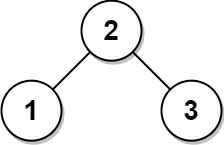
输入: root = [2,1,3]
输出: [2,1,3]

 

提示：

• 树节点的数目在 [1, 104] 范围内。
• 1 <= Node.val <= 105

解题方法：分治

题目给定的二叉搜索树有何特征？

二叉搜索树的中序遍历结果是有序的。

平衡二叉树有何特征？

任一节点左右子树高度差不超过$1$

一个有序节点数组如何建成平衡二叉树？

取数组中点作为根节点，中点左边数组作为左子树，中点右边节点作为右子树，递归建树。

Over。

• 时间复杂度$O(size(tree))$
• 空间复杂度$O(size(tree))$

AC代码

C++

/*
 * @LastEditTime: 2026-02-09 23:21:12
 */
/*
1 2 3 4 5 6 7 8 9

     5
  2     7
1  3   6 8
   4      9
*/
class Solution {
private:
    vector<TreeNode*> nodes;

    void dfs(TreeNode* node) {
        if (!node) {
            return;
        }
        dfs(node->left);
        nodes.push_back(node);
        dfs(node->right);
    }

    TreeNode* build(int l, int r) {
        if (l >= r) {
            return nullptr;
        }
        int mid = (l + r) >> 1;
        TreeNode* root = nodes[mid];
        root->left = build(l, mid);
        root->right = build(mid + 1, r);
        return root;
    }
public:
    TreeNode* balanceBST(TreeNode* root) {
        dfs(root);
        return build(0, nodes.size());
    }
};

#if defined(_WIN32) || defined(__APPLE__)
/*
[1,null,2,null,3,null,4]
*/
int main() {
    string s;
    while (cin >> s) {
        TreeNode* root = stringToTree(s);
        cout << "original tree: " << root << endl;
        Solution sol;
        root = sol.balanceBST(root);
        deleteTree(root);
    }
    return 0;
}
#endif

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源