【LetMeFly】778.水位上升的泳池中游泳：(贪心)优先队列(附C++/Python/Java/Go/Rust优先队列方法表)

力扣题目链接：https://leetcode.cn/problems/swim-in-rising-water/

在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。

当开始下雨时，在时间为 t 时，水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 (0，0) 出发。返回 你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间。

示例 1:

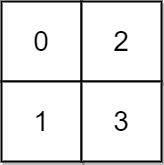
输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为0时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

示例 2:

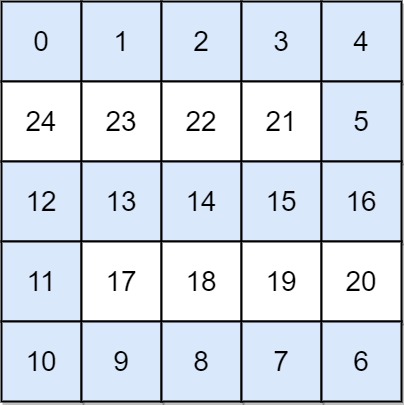
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。
我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的

提示:

n == grid.length
n == grid[i].length
1 <= n <= 50
0 <= grid[i][j] < n²
grid[i][j] 中每个值 均无重复

解题方法：贪心(优先队列)

解题思路

由于你可以在水中瞬移，所以你可以随意地进行尝试，并在发现更优解时瞬移过去继续。

想要找从左上角到右下角最大值尽可能小的一条路，可以使用一个优先队列，把所有的可以走但是还没走到的位置放入优先队列中，然后每次从中取出一个最小的值作为下一步。

具体方法

使用一个布尔类型的数组判断每个位置是否已经走过（贪心策略保证早走一定优于晚走）。使用一个优先队列放入所有可以走到的位置，初始值只有左上角的(0, 0)在优先队列中。

不断从优先队列中取出元素，从当前位置向上下左右四个方向进行尝试，并把没有走过的位置放入优先队列中。入队时更新整条路径中的最高点为当前点和上一个点的最大值。

特别的，一旦右下角的点可走，不用入队再出队了，函数直接返回就好。

思路解析

由于你可以瞬移，所以尝试是不值钱的。哪怕绕18圈也要让一路上的最高点尽可能低。

所以我们采用贪心策略，每次都在下一个能走到的位置中，选一个最低点走过去。

这样走到右下角时，路径的最高点一定是（可能绕来绕去）最低的。

时空复杂度分析

时间复杂度$O(n^2\log n)$
空间复杂度$O(n^2)$

C++/Python/Java/Go/Rust优先队列方法表

语言	数据结构	小顶堆 / 大顶堆	示例代码	说明
C++	`priority_queue`	小顶堆（自定义 comparator）	`auto cmp = [&grid](pair<int,int>& a, pair<int,int>& b) { return grid[a.first][a.second] > grid[b.first][b.second]; // val 小的优先 }; priority_queue<pair<int,int>, vector<pair<int,int>>, decltype(cmp)> pq(cmp); pq.push({0,0});`	使用 lambda 自定义比较函数，小的值优先。
Python	`heapq`	小顶堆（默认）	`import heapq pq = [] heapq.heappush(pq, (grid[0][0], 0, 0)) # (priority, x, y) priority, x, y = heapq.heappop(pq)`	用元组的第一个元素作为优先级，heapq 默认最小堆。
Go	`container/heap`	小顶堆（自定义 Less）	import "container/heap" type Item struct { x, y int priority int } type PriorityQueue []Item func (pq PriorityQueue) Len() int { return len(pq) } func (pq PriorityQueue) Less(i, j int) bool { return pq[i].priority < pq[j].priority } func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] } func (pq PriorityQueue) Push(x any) { pq = append(pq, x.(Item)) } func (pq PriorityQueue) Pop() any { n := len(pq); item := (pq)[n-1]; pq = (pq)[:n-1]; return item } pq := &PriorityQueue{} heap.Init(pq) heap.Push(pq, &Item{x: 0, y: 0, priority: grid[0][0]}) item := heap.Pop(pq).(*Item)	需要自定义类型和接口方法 Len/Swap/Less/Push/Pop。
Java	`PriorityQueue`	小顶堆（自定义 Comparator）	`import java.util.PriorityQueue; PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> grid[a[0]][a[1]] - grid[b[0]][b[1]]); pq.add(new int[]{0, 0}); int[] top = pq.poll(); int x = top[0], y = top[1];`	用数组存坐标对，Comparator 按 grid 值升序。
Rust	`BinaryHeap` + `Reverse`	小顶堆（默认最大堆，需要 Reverse）	`use std::collections::BinaryHeap; use std::cmp::Reverse; let mut pq = BinaryHeap::new(); pq.push(Reverse((grid[0][0], 0, 0))); // Reverse 使最小值优先 if let Some(Reverse((priority, x, y))) = pq.pop() { // 使用 x, y }`	BinaryHeap 默认最大堆，使用 Reverse 包装最小值优先。

AC代码

下面代码实现中，可以处理给定grid不是正方形而是普通长方形的情况。

C++

/*
 * @Author: LetMeFly
 * @Date: 2025-10-06 12:17:42
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-10-06 12:31:27
 */
class Solution {
private:
    static constexpr int direction[4][2] = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
public:
    int swimInWater(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        if (n == 1 && m == 1) {
            return grid[0][0];  // while的判断逻辑是入队时判断是否是终点
        }
        auto cmp = [&grid](pair<int, int>& a, pair<int, int>& b) {
            return grid[a.first][a.second] > grid[b.first][b.second];  // val小的优先
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
        vector<vector<bool>> visited(n, vector<bool>(m));
        pq.push({0, 0});
        visited[0][0] = true;
        while (true) {
            auto [x, y] = pq.top();
            pq.pop();
            for (int d = 0; d < 4; d++) {
                int nx = x + direction[d][0], ny = y + direction[d][1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= m || visited[nx][ny]) {
                    continue;
                }
                grid[nx][ny] = max(grid[nx][ny], grid[x][y]);
                if (nx == n - 1 && ny == m - 1) {
                    return grid[nx][ny];
                }
                visited[nx][ny] = true;
                pq.push({nx, ny});
            }
        }
    }
};

Python

'''
Author: LetMeFly
Date: 2025-10-06 12:17:42
LastEditors: LetMeFly.xyz
LastEditTime: 2025-10-06 13:06:15
'''
from typing import List
import heapq

class Solution:
    directions = [[0, 1], [0, -1], [-1, 0], [1, 0]]

    def swimInWater(self, grid: List[List[int]]) -> int:
        n, m = len(grid), len(grid[0])
        if n == 1 and m == 1:
            return grid[0][0]
        visited = [[False] * m for _ in range(n)]
        pq = [(grid[0][0], 0, 0)]
        visited[0][0] = True
        while True:
            val, x, y = heapq.heappop(pq)
            for dx, dy in self.directions:
                nx, ny = x + dx, y + dy
                if (not (0 <= nx < n and 0 <= ny < m)) or visited[nx][ny]:
                    continue
                grid[nx][ny] = max(grid[nx][ny], val)
                if nx == n - 1 and ny == m - 1:
                    return grid[nx][ny]
                visited[nx][ny] = True
                heapq.heappush(pq, (grid[nx][ny], nx, ny))

Java

/*
 * @Author: LetMeFly
 * @Date: 2025-10-06 12:17:42
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-10-06 14:04:24
 */
import java.util.PriorityQueue;

class Solution {
    private static final int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    public int swimInWater(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        if (n == 1 && m == 1) {
            return grid[0][0];
        }
        boolean[][] visited = new boolean[n][m];
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> grid[a[0]][a[1]] - grid[b[0]][b[1]]);
        pq.add(new int[]{0, 0});
        visited[0][0] = true;
        while (true) {
            int[] top = pq.poll();
            int x = top[0], y = top[1];
            for (int[] d : directions) {
                int nx = x + d[0], ny = y + d[1];
                if (nx < 0 || nx >= n || ny < 0 || ny >= m || visited[nx][ny]) {
                    continue;
                }
                grid[nx][ny] = Math.max(grid[nx][ny], grid[x][y]);
                if (nx == n - 1 && ny == m - 1) {
                    return grid[nx][ny];
                }
                visited[nx][ny] = true;
                pq.add(new int[]{nx, ny});
            }
        }
    }
}

Go

/*
 * @Author: LetMeFly
 * @Date: 2025-10-06 12:17:42
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-10-06 14:31:37
 */
package main

import "container/heap"

type Item778 struct {
    x, y int
    val int
}

type PriorityQueue778 []*Item778

var directions778 = [][]int{{0, 1}, {0, -1}, {-1, 0}, {1, 0}}

func swimInWater(grid [][]int) int {
    n, m := len(grid), len(grid[0])
    if n == 1 && m == 1 {
        return grid[0][0]
    }
    visited := make([][]bool, n)
    for i, _ := range visited {
        visited[i] = make([]bool, m)
    }

    pq := &PriorityQueue778{}
    heap.Init(pq)
    heap.Push(pq, &Item778{0, 0, grid[0][0]})
    visited[0][0] = true
    for true {
        item := heap.Pop(pq).(*Item778)
        x, y, val := item.x, item.y, item.val
        for _, d := range directions778 {
            nx, ny := x + d[0], y + d[1]
            if nx < 0 || nx >= n || ny < 0 || ny >= m || visited[nx][ny] {
                continue
            }
            grid[nx][ny] = max(grid[nx][ny], val)
            if nx == n - 1 && ny == m - 1 {
                return grid[nx][ny]
            }
            visited[nx][ny] = true
            heap.Push(pq, &Item778{nx, ny, grid[nx][ny]})
        }
    }

    return -1  // Fake Return
}

func (pq PriorityQueue778) Len() int { return len(pq) }
func (pq PriorityQueue778) Less(i, j int) bool { return pq[i].val < pq[j].val }
func (pq PriorityQueue778) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue778) Push(x any) { *pq = append(*pq, x.(*Item778)) }
func (pq *PriorityQueue778) Pop() any { n := len(*pq); item := (*pq)[n - 1]; *pq = (*pq)[:n-1]; return item }

Rust

/*
 * @Author: LetMeFly
 * @Date: 2025-10-06 12:17:42
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-10-06 14:48:19
 */
use std::collections::BinaryHeap;
use std::cmp::Reverse;

impl Solution {
    const DIRECTIONS: [[i32; 2]; 4] = [[0, 1], [0, -1], [-1, 0], [1, 0]];
    pub fn swim_in_water(grid: Vec<Vec<i32>>) -> i32 {
        let n: usize = grid.len();
        let m: usize = grid[0].len();
        if n == 1 && m == 1 {
            return grid[0][0];
        }
        let mut pq = BinaryHeap::new();
        let mut visited: Vec<Vec<bool>> = vec![vec![false; m]; n];
        pq.push(Reverse((grid[0][0], 0, 0)));
        visited[0][0] = true;

        while let Some(Reverse((val, x, y))) = pq.pop() {
            for &[dx, dy] in Self::DIRECTIONS.iter() {
                let nx: usize = x + dx as usize;  // 这样写其实不好，x+dx<0时nx会溢出变成很大的数（一定大于n）
                let ny: usize = y + dy as usize;  // 所以结果正确但其实代码有点迷惑
                if nx < 0 || nx >= n || ny < 0 || ny >= m || visited[nx][ny] {
                    continue;
                }
                let n_val: i32 = val.max(grid[nx][ny]);
                if nx == n - 1 && ny == m - 1 {
                    return n_val;
                }
                visited[nx][ny] = true;
                pq.push(Reverse((n_val, nx, ny)));
            }
        }

        -1  // Fake Return
    }
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源

题解 > LeetCode

#题解 #数组 #LeetCode #困难 #堆（优先队列） #优先队列 #深度优先搜索 #矩阵 #堆

778.水位上升的泳池中游泳：(贪心)优先队列(附C++/Python/Java/Go/Rust优先队列方法表)

https://blog.letmefly.xyz/2025/10/06/LeetCode 0778.水位上升的泳池中游泳/

作者

Tisfy

发布于

2025年10月6日

许可协议

3494.酿造药水需要的最少总时间：模拟(贪心)——一看就懂的描述上一篇

1039.多边形三角剖分的最低得分：记忆化搜索（深度优先搜索）下一篇