3459.最长 V 形对角线段的长度：记忆化搜索——就一步步试

【LetMeFly】3459.最长 V 形对角线段的长度：记忆化搜索——就一步步试

力扣题目链接：https://leetcode.cn/problems/length-of-longest-v-shaped-diagonal-segment/

给你一个大小为 n x m 的二维整数矩阵 grid，其中每个元素的值为 0、1 或 2。

V 形对角线段 定义如下：

  • 线段从 1 开始。
  • 后续元素按照以下无限序列的模式排列：2, 0, 2, 0, ...。
  • 该线段：
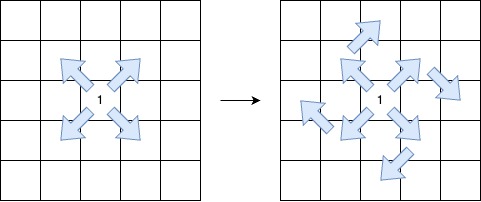
    • 起始于某个对角方向（左上到右下、右下到左上、右上到左下或左下到右上）。
    • 沿着相同的对角方向继续，保持 序列模式 。
    • 在保持 序列模式 的前提下，最多允许 一次顺时针 90 度转向 另一个对角方向。

返回最长的 V 形对角线段 的 长度 。如果不存在有效的线段，则返回 0。

 

示例 1：

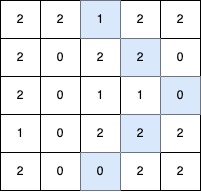
输入： grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 5

解释：

最长的 V 形对角线段长度为 5，路径如下：(0,2) → (1,3) → (2,4)，在 (2,4) 处进行 顺时针 90 度转向 ，继续路径为 (3,3) → (4,2)。

示例 2：

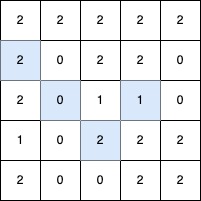
输入： grid = [[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

输出： 4

解释：

最长的 V 形对角线段长度为 4，路径如下：(2,3) → (3,2)，在 (3,2) 处进行 顺时针 90 度转向 ，继续路径为 (2,1) → (1,0)。

示例 3：

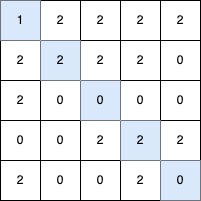
输入： grid = [[1,2,2,2,2],[2,2,2,2,0],[2,0,0,0,0],[0,0,2,2,2],[2,0,0,2,0]]

输出： 5

解释：

最长的 V 形对角线段长度为 5，路径如下：(0,0) → (1,1) → (2,2) → (3,3) → (4,4)。

示例 4：

输入： grid = [[1]]

输出： 1

解释：

最长的 V 形对角线段长度为 1，路径如下：(0,0)。

 

提示：

  • n == grid.length
  • m == grid[i].length
  • 1 <= n, m <= 500
  • grid[i][j] 的值为 0、1 或 2。

解题方法：记忆化搜索

解题思路

题目翻译：从一个位置出发沿4个45度倾斜的方向移动，最多右转一次，起点一定是1，经过路径一定是2020...(不能是0202..)，求最长路径是多少。

写一个函数dfs(int i, int j, int d, int times)，代表当前位置坐标为(i, j)、前进方向为d、拐弯了times次的状态下，算上当前位置的最长路径长度。

如果沿当前方向向前走能继续走，那就尝试；如果右转90度能继续走，那就也试试。终止条件：一定会走到走不动为止。

那么，所有grid[i][j] == 1的下标(i, j)，4个方向且times为0的初始状态的到的最大结果即为答案。

然后记得记忆化一下，算过的(i, j, d, times)不要再重复计算一次。

具体方法

实际编码的时候，给定的数据量在使用默认的缓存时可能会TLE或OOM。所以C++和Python要使用数组手动记忆化一下。

如何将(i, j, d, times)映射为一个下标？i * m * 8 + j * 8 + d * 2 + times即可。

剪枝(可选)

有没有可以提前退出的时刻？有，可以维护一个“全局”的最长路径，若当前状态一直往前走无论如何也无法超过历史最优解，索性放弃尝试，及时止损

时空复杂度分析

  • 时间复杂度$O(mn)$
  • 空间复杂度$O(mn)$

其实时空复杂度都要乘上一个常数8。

AC代码

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
/*
 * @Author: LetMeFly
 * @Date: 2025-08-27 23:08:01
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-08-29 18:50:39
 */
#if defined(_WIN32) || defined(__APPLE__)
#include "_[1,2]toVector.h"
#endif

#define dbgIJDT(msg) printf("dbg(%s): i == %d && j == %d && d == %d && times == %d\n", msg, i, j, d, times)

// 有点卡极限 数据范围似乎不是很好
class Solution {
private:
    const int directions[4][2] = {
        {1, 1},    // 0 - ↘️
        {1, -1},   // 1 - ↙️
        {-1, -1},  // 2 - ↖️
        {-1, 1}    // 3 - ↗️
    };
    vector<vector<int>> grid;
    vector<int> cache;
    int n, m;

    inline bool canContinue(int i, int j, int ni, int nj) {
        if (!(ni >= 0 && ni < n && nj >= 0 && nj < m)) {
            return false;
        }
        int thisVal = grid[i][j], nextVal = grid[ni][nj];
        return (thisVal == 1 && nextVal == 2) || (thisVal != 1 && nextVal != 1 && thisVal != nextVal);
    }

    /*
    >>> 500 * 500
    250000
    >>> 500 * 500 * 4 * 2
    2000000
    >>> 500 * 4 * 2
    4000
    >>> 4 * 2
    8
    */
    inline int getCacheKey(int i, int j, int d, int times) {
        return i * 8 * m + j * 8 + d * 2 + times;
    }

    int dfs(int i, int j, int d, int times) {
        int cacheKey = getCacheKey(i, j, d, times);
        // if (cacheKey == 12018) {
        //     dbgIJDT("cacheKey=12018");
        // }
        if (cache[cacheKey] != -1) {
            return cache[cacheKey];
        }
        int toAdd = 0;
        int ni = i + directions[d][0], nj = j + directions[d][1];
        // if (i == 2 && j == 1 && d == 2 && times == 1 || i == 3 && j == 2 && d == 1 && times == 0 || i == 2 && j == 3 && d == 1 && times == 0) {
        //     dbgIJDT("after cache");
        // }
        if (canContinue(i, j, ni, nj)) {
            toAdd = dfs(ni, nj, d, times);
        }
        if (times == 0) {
            int nd = (d + 1) % 4;
            int ni = i + directions[nd][0], nj = j + directions[nd][1];
            if (canContinue(i, j, ni, nj)) {
                toAdd = max(toAdd, dfs(ni, nj, nd, 1));
            }
        }
        return cache[cacheKey] = 1 + toAdd;
    }
public:
    int lenOfVDiagonal(vector<vector<int>>& grid) {
        this->grid = move(grid);
        n = this->grid.size(), m = this->grid[0].size();
        cache.resize(m * n * 8, -1);
        int ans = 0;
        for (int i = 0; i < this->n; i++) {
            for (int j = 0; j < this->grid[i].size(); j++) {
                if (this->grid[i][j] != 1) {
                    continue;
                }
                for (int d = 0; d < 4; d++) {
                    ans = max(ans, dfs(i, j, d, 0));
                }
            }
        }
        return ans;
    }
};

#if defined(_WIN32) || defined(__APPLE__)
/*
[[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

5
*/
/*
[[2,2,2,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]

4
*/
/*
[[1,2,2],[1,0,2]]


1 2 2
1 0 2

2
*/
/*
[[2,2,0,2,0,2,0],[1,2,2,1,0,2,0]]

2 2 0 2 0 2 0
1 2 2 1 0 2 0

2
*/
int main() {
    string s;
    while (cin >> s) {
        vector<vector<int>> v = stringToVectorVector(s);
        Solution sol;
        cout << sol.lenOfVDiagonal(v) << endl;
    }
    return 0;
}
#endif

AC,64.08%,42.73%

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
'''
Author: LetMeFly
Date: 2025-08-28 12:54:06
LastEditors: LetMeFly.xyz
LastEditTime: 2025-08-31 19:11:00
'''
from typing import List

class Solution:
    directions = [
        [1, 1],
        [1, -1],
        [-1, -1],
        [-1, 1]
    ]

    """
    canContinue只考虑从(i, j)开始能否沿着方向d走一步
    """
    def canContinue(self, i: int, j: int, d: int) -> bool:
        ni, nj = i + self.directions[d][0], j + self.directions[d][1]
        if ni < 0 or ni >= self.n or nj < 0 or nj >= self.m:
            return False
        now = self.grid[i][j]
        next = self.grid[ni][nj]
        return now == 1 and next == 2 or now != 1 and next != 1 and now != next
    
    def getCacheKey(self, i: int, j: int, d: int, canChange: bool) -> int:
        return i * self.m * 8 + j * 8 + d * 2 + canChange

    def dfs(self, i: int, j: int, d: int, canChange: bool) -> int:
        cacheKey = self.getCacheKey(i, j, d, canChange)
        if self.cache[cacheKey] != -1:
            return self.cache[cacheKey]
        then = 0
        if self.canContinue(i, j, d):
            then = self.dfs(i + self.directions[d][0], j + self.directions[d][1], d, canChange)
        if canChange:
            nd = (d + 1) % 4
            if self.canContinue(i, j, nd):
                then = max(then, self.dfs(i + self.directions[nd][0], j + self.directions[nd][1], nd, False))
        self.cache[cacheKey] = then + 1
        return then + 1

    def lenOfVDiagonal(self, grid: List[List[int]]) -> int:
        self.grid = grid
        self.n, self.m = len(grid), len(grid[0])
        self.cache = [-1] * (self.m * self.n * 8)
        ans = 0
        for i, line in enumerate(grid):
            for j, g in enumerate(line):
                if g != 1:
                    continue
                for d in range(4):
                    ans = max(ans, self.dfs(i, j, d, True))
        return ans


if __name__ == '__main__':
    from functools import cache
    class A:
        def __init__(self, x):
            self.x = x

        @cache
        def f(self, y):
            print("running f...")
            return self.x + y


    a1 = A(10)
    a2 = A(20)

    print(a1.f(1))  # 运行函数，输出 11
    print(a1.f(1))  # 命中缓存，直接输出 11
    print(a2.f(1))  # 不命中缓存，输出21

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源

题解 > LeetCode
#题解 #数组 #LeetCode #困难 #深度优先搜索 #DFS #矩阵 #记忆化搜索
3459.最长 V 形对角线段的长度：记忆化搜索——就一步步试
https://blog.letmefly.xyz/2025/08/31/LeetCode 3459.最长V形对角线段的长度/
作者
发布于
2025年8月31日
许可协议