2116.判断一个括号字符串是否有效：括号匹配(两个变量一次遍历解决)

【LetMeFly】2116.判断一个括号字符串是否有效：括号匹配(两个变量一次遍历解决)

力扣题目链接：https://leetcode.cn/problems/check-if-a-parentheses-string-can-be-valid/

一个括号字符串是只由 '(' 和 ')' 组成的 非空 字符串。如果一个字符串满足下面 任意 一个条件，那么它就是有效的：

• 字符串为 ().
• 它可以表示为 AB（A 与 B 连接），其中A 和 B 都是有效括号字符串。
• 它可以表示为 (A) ，其中 A 是一个有效括号字符串。

给你一个括号字符串 s 和一个字符串 locked ，两者长度都为 n 。locked 是一个二进制字符串，只包含 '0' 和 '1' 。对于 locked 中 每一个 下标 i ：

• 如果 locked[i] 是 '1' ，你 不能 改变 s[i] 。
• 如果 locked[i] 是 '0' ，你 可以 将 s[i] 变为 '(' 或者 ')' 。

如果你可以将 s 变为有效括号字符串，请你返回 true ，否则返回 false 。

 

示例 1：

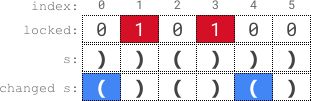
输入：s = "))()))", locked = "010100"
输出：true
解释：locked[1] == '1' 和 locked[3] == '1' ，所以我们无法改变 s[1] 或者 s[3] 。
我们可以将 s[0] 和 s[4] 变为 '(' ，不改变 s[2] 和 s[5] ，使 s 变为有效字符串。

示例 2：

输入：s = "()()", locked = "0000"
输出：true
解释：我们不需要做任何改变，因为 s 已经是有效字符串了。

示例 3：

输入：s = ")", locked = "0"
输出：false
解释：locked 允许改变 s[0] 。
但无论将 s[0] 变为 '(' 或者 ')' 都无法使 s 变为有效字符串。

 

提示：

• n == s.length == locked.length
• 1 <= n <= 105
• s[i] 要么是 '(' 要么是 ')' 。
• locked[i] 要么是 '0' 要么是 '1' 。

很不错的一道题，这题灵茶山艾府的题解很棒。

解题方法：一次遍历(贪心)

解题思路

整个遍历过程中，要时刻保证：

• 左括号的数量始终不少于右括号的数量

遍历结束后，要保证左括号的数量和右括号的数量相等。

我们可以使用$diff$来表示左括号的数量减去右括号的数量的差值，则想要返回true必须满足：

1. 遍历过程中始终有：$diff\geq 0$
2. 遍历结束时，$diff = 0$

如果每个字符都是确定的话还好说，但是有的字符可以更改（locked[i] = '0'）要怎么处理呢？

其实也很简单，是(是)都试试呗。不难发现：

假设$diff=3$时遇到了一个locked[i] = '0'，那么s[i]为(的话$diff$将变成$4$，s[i]为)的话$diff$将变成$6$。$diff$的取值范围变成了${4, 6}$（全为偶数）

在此基础上，假设又遇到了locked[i] = '0'，那么s[i]为(的话$diff$将变成${3, 5}$，s[i]为)的话$diff$将变成${5, 7}$。$diff$的取值范围变成了${3, 5, 7}$（全是奇数）

不难发现$diff$的取值范围要么是全奇数，要么是全偶数。所以可以用$l$表示$diff$合法取值范围的最小值，$r$表示$diff$合法取值范围的最大值。

具体做法

初始值$l = 0, r = 0$，代表(和)差值的可能范围为${0}$。

开始遍历字符串：

• 如果locked[i] = '0'，说明可(可)，范围将变成l - 1到r + 1

  注意如果l变成了-1则说明l本来是0，要将l重新置为合法范围1

• 否则（locked[i] = '1'）

  • 如果s[i] = '('：范围将变成l + 1到r + 1

  • 否则(s[i] = ')')：范围将变成l - 1到r - 1

    此时如果r < 0，则说明合法范围为空，不满足“整个遍历过从始终有$diff\geq 0$”，直接返回false

    此时如果l < 0（l变成了-1），则说明l本来是0，要将l重新置为合法范围1

最终，若l为0则说存在(和)相等的情况，返回true。

时空复杂度

• 时间复杂度$O(len(s))$
• 空间复杂度$O(1)$

AC代码

C++

/*
 * @Author: LetMeFly
 * @Date: 2025-03-23 09:37:28
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-03-23 10:39:28
 */
#ifdef _WIN32
#include "_[1,2]toVector.h"
#endif

/*
*)*(**
()(())


(*)*
(())


(**(
xxxx

(*
()



*/
class Solution {
public:
    bool canBeValid(string s, string locked) {
        int l = 0, r = 0;
        for (int i = 0; i < s.size(); i++) {
            if (locked[i] == '0') {
                l--, r++;
                if (l < 0) {
                    l = 1;
                }
            } else {  // ()
                if (s[i] == '(') {
                    l++, r++;
                } else {
                    l--, r--;
                    if (r < 0) {
                        return false;
                    }
                    if (l < 0) {
                        l = 1;
                    }
                }
            }
        }
        return !l;
    }
};

Python

'''
Author: LetMeFly
Date: 2025-03-23 10:49:44
LastEditors: LetMeFly.xyz
LastEditTime: 2025-03-23 10:51:19
'''
class Solution:
    def canBeValid(self, s: str, locked: str) -> bool:
        l = r = 0
        for i in range(len(s)):
            if locked[i] == '0':
                l -= 1
                r += 1
                if l == -1:
                    l = 1
            else:
                if s[i] == '(':
                    l += 1
                    r += 1
                else:
                    l -= 1
                    r -= 1
                    if r < 0:
                        return False
                    if l < 0:
                        l = 1
        return not l

Java

/*
 * @Author: LetMeFly
 * @Date: 2025-03-23 10:52:22
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-03-23 10:53:49
 */
class Solution {
    public boolean canBeValid(String s, String locked) {
        int l = 0, r = 0;
        for (int i = 0; i < s.length(); i++) {
            if (locked.charAt(i) == '0') {
                l--;
                r++;
                if (l < 0) {
                    l = 1;
                }
            } else {
                if (s.charAt(i) == '(') {
                    l++;
                    r++;
                } else {
                    l--;
                    r--;
                    if (r < 0) {
                        return false;
                    }
                    if (l < 0) {
                        l = 1;
                    }
                }
            }
        }
        return l == 0;
    }
}

Go

/*
 * @Author: LetMeFly
 * @Date: 2025-03-23 10:54:53
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-03-23 10:56:04
 */
package main

func canBeValid(s string, locked string) bool {
    l, r := 0, 0
    for i := range s {
        if locked[i] == '0' {
            l--
            r++
            if l < 0 {
                l = 1
            }
        } else {
            if s[i] == '(' {
                l++
                r++
            } else {
                l--
                r--
                if r < 0 {
                    return false
                }
                if l < 0 {
                    l = 1
                }
            }
        }
    }
    return l == 0
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源