3219.切蛋糕的最小总开销 II

【LetMeFly】3219.切蛋糕的最小总开销 II：贪心——先切贵的

力扣题目链接：https://leetcode.cn/problems/minimum-cost-for-cutting-cake-ii/

有一个 m x n 大小的矩形蛋糕，需要切成 1 x 1 的小块。

给你整数 m ，n 和两个数组：

• horizontalCut 的大小为 m - 1 ，其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
• verticalCut 的大小为 n - 1 ，其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。

一次操作中，你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一：

1. 沿着水平线 i 切开蛋糕，开销为 horizontalCut[i] 。
2. 沿着垂直线 j 切开蛋糕，开销为 verticalCut[j] 。

每次操作后，这块蛋糕都被切成两个独立的小蛋糕。

每次操作的开销都为最开始对应切割线的开销，并且不会改变。

请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。

 

示例 1：

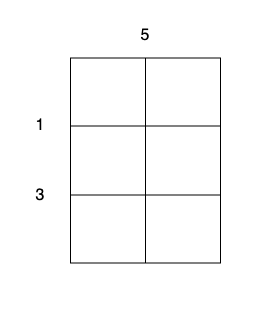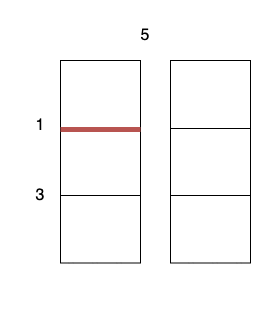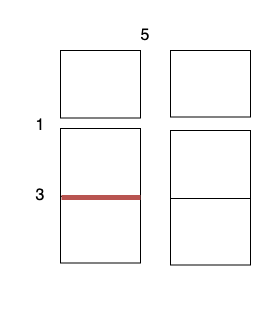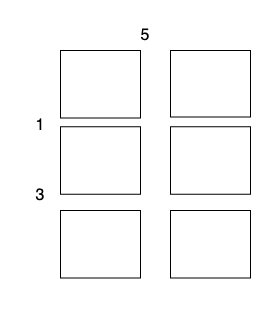
输入：m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

输出：13

解释：

• 沿着垂直线 0 切开蛋糕，开销为 5 。
• 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
• 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
• 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。
• 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。

总开销为 5 + 1 + 1 + 3 + 3 = 13 。

示例 2：

输入：m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

输出：15

解释：

• 沿着水平线 0 切开蛋糕，开销为 7 。
• 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。
• 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。

总开销为 7 + 4 + 4 = 15 。

 

提示：

• 1 <= m, n <= 105
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 103

解题方法：贪心（双指针）

从头到尾贯穿整个蛋糕的一刀切的越早，所需的切割次数越少。

例如假如一个2x2的蛋糕：

1. 先竖着切，就是竖着一刀横着两刀
2. 先横着切，就是竖着两刀横着一刀

所以，将切割代价按照从大到小的顺序排序，然后在横竖切法里挑最贵的先切就好了。

切的时候从头切到尾：

假如这是竖着的一刀，就看横向一共切了几次。

如果横向一共切了$hCutTime$次，那么这一刀就要切$hCutTime + 1$次。

• 时间复杂度$O(m\log m + n\log n)$
• 空间复杂度$O(\log m + \log n)$

AC代码

C++

/*
 * @Author: LetMeFly
 * @Date: 2024-12-31 13:04:36
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-31 13:10:03
 */
#ifdef _WIN32
#include "_[1,2]toVector.h"
#endif

typedef long long ll;
class Solution {
public:
    ll minimumCost(int m, int n, vector<int>& horizontalCut, vector<int>& verticalCut) {
        sort(horizontalCut.begin(), horizontalCut.end(), greater<>());
        sort(verticalCut.begin(), verticalCut.end(), greater<>());
        int hCutTime = 0, vCutTime = 0;
        ll ans = 0;
        while (hCutTime < horizontalCut.size() || vCutTime < verticalCut.size()) {
            if (vCutTime == verticalCut.size() || hCutTime < horizontalCut.size() && horizontalCut[hCutTime] > verticalCut[vCutTime]) {
                ans += horizontalCut[hCutTime++] * (vCutTime + 1);
            } else {
                ans += verticalCut[vCutTime++] * (hCutTime + 1);
            }
        }
        return ans;
    }
};

Python

'''
Author: LetMeFly
Date: 2024-12-31 13:10:50
LastEditors: LetMeFly.xyz
LastEditTime: 2024-12-31 13:14:10
'''
from typing import List

class Solution:
    def minimumCost(self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]) -> int:
        horizontalCut.sort(key=lambda a: -a)
        verticalCut.sort(key=lambda a: -a)
        ans = hCutTime = vCutTime = 0
        m, n = m - 1, n - 1
        while hCutTime < m or vCutTime < n:
            if vCutTime == n or hCutTime < m and horizontalCut[hCutTime] > verticalCut[vCutTime]:
                ans += horizontalCut[hCutTime] * (vCutTime + 1)
                hCutTime += 1
            else:
                ans += verticalCut[vCutTime] * (hCutTime + 1)
                vCutTime += 1
        return ans

Java

/*
 * @Author: LetMeFly
 * @Date: 2024-12-31 13:14:31
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-31 13:22:22
 */
import java.util.Arrays;

class Solution {
    public long minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
        // Arrays.sort(horizontalCut, (a, b) -> b - a);  // 不可，Arrays.sort(int[])时不支持自定义排序
        Arrays.sort(horizontalCut);  // 那就从小到大排序然后下面反着遍历吧
        Arrays.sort(verticalCut);
        int hCutTime = m - 2, vCutTime = n - 2;
        long ans = 0;
        while (hCutTime >= 0 || vCutTime >= 0) {
            if (vCutTime < 0 || hCutTime >= 0 && horizontalCut[hCutTime] > verticalCut[vCutTime]) {
                ans += horizontalCut[hCutTime--] * (n - vCutTime - 1);
            } else {
                ans += verticalCut[vCutTime--] * (m - hCutTime - 1);
            }
        }
        return ans;
    }
}

Go

/*
 * @Author: LetMeFly
 * @Date: 2024-12-31 13:23:11
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-31 13:37:03
 */
package main

import "slices"

func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) (ans int64) {
    slices.SortFunc(horizontalCut, func(i, j int) int { return j - i; });
    slices.SortFunc(verticalCut, func(i, j int) int { return j - i; });
    var hCutTime, vCutTime int
    m, n = m - 1, n - 1
    for hCutTime < m || vCutTime < n {
        if vCutTime == n || hCutTime < m && horizontalCut[hCutTime] > verticalCut[vCutTime] {
            ans += int64(horizontalCut[hCutTime] * (vCutTime + 1))
            hCutTime++
        } else {
            ans += int64(verticalCut[vCutTime] * (hCutTime + 1))
            vCutTime++
        }
    }
    return
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/144849684