【LetMeFly】2101.引爆最多的炸弹:深度优先搜索(DFS)
力扣题目链接:https://leetcode.cn/problems/detonate-the-maximum-bombs/
给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。
炸弹用一个下标从 0 开始的二维整数数组 bombs 表示,其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标,ri 表示爆炸范围的 半径 。
你需要选择引爆 一个 炸弹。当这个炸弹被引爆时,所有 在它爆炸范围内的炸弹都会被引爆,这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。
给你数组 bombs ,请你返回在引爆 一个 炸弹的前提下,最多 能引爆的炸弹数目。
示例 1:
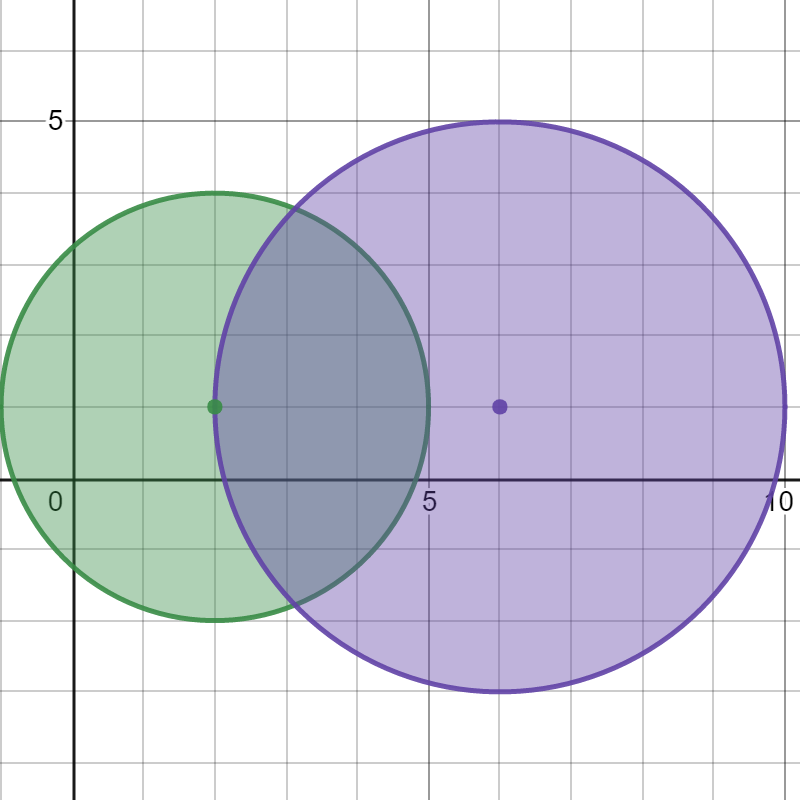
输入:bombs = [[2,1,3],[6,1,4]]
输出:2
解释:
上图展示了 2 个炸弹的位置和爆炸范围。
如果我们引爆左边的炸弹,右边的炸弹不会被影响。
但如果我们引爆右边的炸弹,两个炸弹都会爆炸。
所以最多能引爆的炸弹数目是 max(1, 2) = 2 。
示例 2:
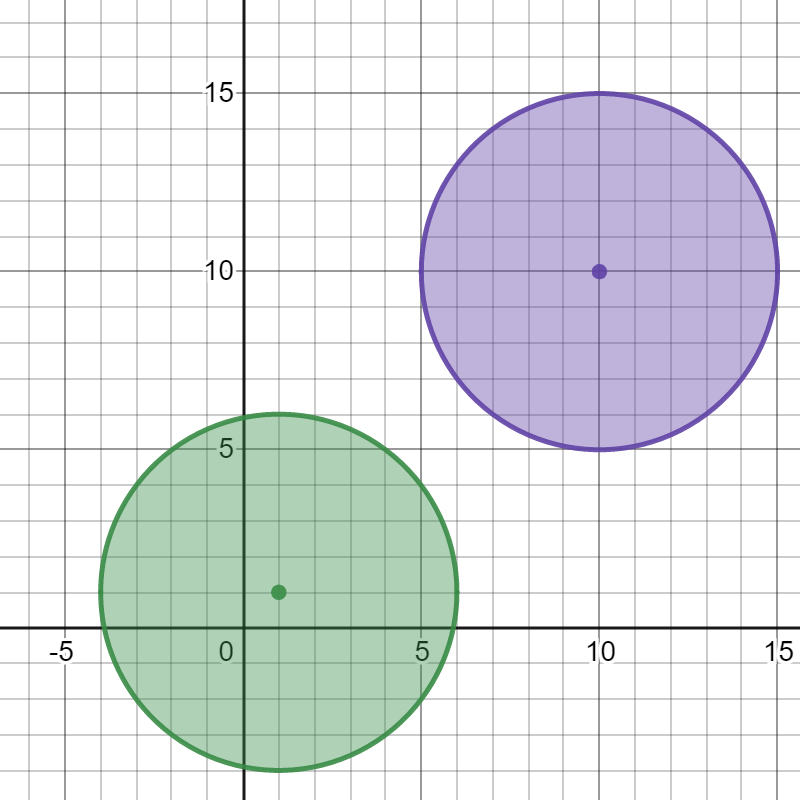
输入:bombs = [[1,1,5],[10,10,5]]
输出:1
解释:
引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。
示例 3:

输入:bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
输出:5
解释:
最佳引爆炸弹为炸弹 0 ,因为:
- 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。
- 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。
- 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。
所以总共有 5 个炸弹被引爆。
提示:
1 <= bombs.length <= 100bombs[i].length == 31 <= xi, yi, ri <= 105
解题方法:深度优先搜索
首先,我们可以以每个炸弹为点建立一个有向图。如果炸弹i能引爆炸弹j,则建立一条由i指向j的边。两层循环遍历炸弹数组即可完成建图。(细节:可以使用距离的平方和半径的平方进行比较从而避免浮点数的出现)
有了这个图之后,我们就可以开始愉快地深搜了。以任意一个炸弹为起点开始深搜,搜索所有这个炸弹能到达的位置,即为点燃这个炸弹能引爆的所有炸弹的数量。从每个炸弹开始深搜,最大的能引爆数量即为所求。
- 时间复杂度$O(len(bombs)^3)$,单次搜索复杂度最高可以达到$O(n^2)$
- 空间复杂度$O(n^2)$,全连接图可以达到$O(n^2)$的空间复杂度
进阶: 有没有发现在搜索过程中很多计算是重复的?有没有方法避免?使用拓扑排序的变种?
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| typedef long long ll;
class Solution {
private:
vector<bool> visited;
vector<vector<int>> graph;
int dfs(int x) {
visited[x] = true;
int ans = 1;
for (int nextNode : graph[x]) {
if (!visited[nextNode]) {
ans += dfs(nextNode);
}
}
return ans;
}
public:
int maximumDetonation(vector<vector<int>>& bombs) {
int n = bombs.size();
graph = vector<vector<int>>(n);
for (int i = 0; i < bombs.size(); i++) {
for (int j = i + 1; j < bombs.size(); j++) {
ll d2 = (ll)(bombs[i][0] - bombs[j][0]) * (bombs[i][0] - bombs[j][0]) + (ll)(bombs[i][1] - bombs[j][1]) * (bombs[i][1] - bombs[j][1]);
if (d2 <= (ll)bombs[i][2] * bombs[i][2]) {
graph[i].push_back(j);
}
if (d2 <= (ll)bombs[j][2] * bombs[j][2]) {
graph[j].push_back(i);
}
}
}
int ans = 1;
for (int i = 0; i < n; i++) {
visited = vector<bool>(n);
ans = max(ans, dfs(i));
}
return ans;
}
};
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| from typing import List
class Solution:
def dfs(self, x: int) -> int:
self.visited[x] = True
ans = 1
for nextNode in self.graph[x]:
if not self.visited[nextNode]:
ans += self.dfs(nextNode)
return ans
def maximumDetonation(self, bombs: List[List[int]]) -> int:
self.graph = [[] for _ in range(len(bombs))]
for i in range(len(bombs)):
for j in range(i + 1, len(bombs)):
d2 = (bombs[i][0] - bombs[j][0]) * (bombs[i][0] - bombs[j][0]) + (bombs[i][1] - bombs[j][1]) * (bombs[i][1] - bombs[j][1])
if d2 <= bombs[i][2] * bombs[i][2]:
self.graph[i].append(j)
if d2 <= bombs[j][2] * bombs[j][2]:
self.graph[j].append(i)
ans = 1
for i in range(len(bombs)):
self.visited = [False] * len(bombs)
ans = max(ans, self.dfs(i))
return ans
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| package main
var visited []bool
var graph [][]int
func max(a int, b int) int {
if a > b {
return a
}
return b
}
func dfs(x int) int {
visited[x] = true
ans := 1
for _, nextNode := range graph[x] {
if !visited[nextNode] {
ans += dfs(nextNode)
}
}
return ans
}
func maximumDetonation(bombs [][]int) int {
n := len(bombs)
graph = make([][]int, n)
for i := 0; i < n; i++ {
for j := i + 1; j < n; j++ {
d2 := (int64)(bombs[i][0] - bombs[j][0]) * (int64)(bombs[i][0] - bombs[j][0]) + (int64)(bombs[i][1] - bombs[j][1]) * (int64)(bombs[i][1] - bombs[j][1])
if d2 <= (int64)(bombs[i][2]) * (int64)(bombs[i][2]) {
graph[i] = append(graph[i], j)
}
if d2 <= (int64)(bombs[j][2]) * (int64)(bombs[j][2]) {
graph[j] = append(graph[j], i)
}
}
}
ans := 1
for i := 0; i < n; i++ {
visited = make([]bool, n)
ans = max(ans, dfs(i))
}
return ans
}
|
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
class Solution {
private boolean[] visited;
private List<Integer>[] graph;
private int dfs(int x) {
visited[x] = true;
int ans = 1;
for (int nextNode : graph[x]) {
if (!visited[nextNode]) {
ans += dfs(nextNode);
}
}
return ans;
}
public int maximumDetonation(int[][] bombs) {
int n = bombs.length;
graph = new ArrayList[n];
Arrays.setAll(graph, thisArray -> new ArrayList<>());
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
long d2 = (long)(bombs[i][0] - bombs[j][0]) * (bombs[i][0] - bombs[j][0]) + (long)(bombs[i][1] - bombs[j][1]) * (bombs[i][1] - bombs[j][1]);
if (d2 <= (long)bombs[i][2] * bombs[i][2]) {
graph[i].add(j);
}
if (d2 <= (long)bombs[j][2] * bombs[j][2]) {
graph[j].add(i);
}
}
}
int ans = 1;
for (int i = 0; i < n; i++) {
visited = new boolean[n];
ans = Math.max(ans, dfs(i));
}
return ans;
}
}
|
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/140629296


