1483.树节点的第 K 个祖先

【LetMeFly】1483.树节点的第 K 个祖先：树上倍增

力扣题目链接：https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

• TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
• getKthAncestor(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

 

示例 1：

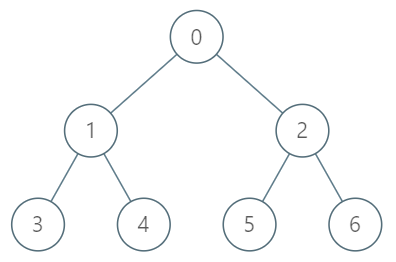
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]

输出：
[null,1,0,-1]

解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);

treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

 

提示：

• 1 <= k <= n <= 5 * 104
• parent[0] == -1 表示编号为 0 的节点是根节点。
• 对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
• 0 <= node < n
• 至多查询 5 * 104 次

解题方法：树上倍增

预处理并创建一个anc数组，令anc[i][j]为节点i的第$2^j$个祖先。（其中anc是ancestors的缩写）

这样就剩下了两个问题：

问题一、如何创建anc数组

首先anc[i][0] = parent[i]（$2^0=1$，节点i的第1个祖先为其父节点）

其次j > 1时anc[i][j] = anc[ anc[i][j-1] ][j-1]（例如节点i的第8祖先节点 等于 节点i的第4祖先节点的第4祖先节点）

并且有anc[-1][*] = -1（已经无祖先节点了，再往上跳还是-1）

由于$2^{16}=65536\gt 50000$，因此最多$\log n=16$次就能完成一个节点的所有$2^j$祖先数组。

问题二、如何依据anc数组快速求得节点node的第k祖先

假设要求节点node的第$k=5=101_2=4+1$祖先节点，那么可以求node的第1父节点的第4父节点，也就是说anc[ anc[node][0] ][2]即为答案。

因此，我们可以从低到高（从高到低也一样）遍历k的二进制位，如果第j位为1，则令node = anc[node][j]，即求node的$2^j$祖先节点。

特别的，若node已经为-1则可直接返回。

时空复杂度

• 时间复杂度：初始化$O(n\log n)$，单次查询$O(\log n)$
• 空间复杂度：初始化$O(n\log n)$，单次查询$O(1)$

AC代码

C++

class TreeAncestor {
private:
    const static int Log = 16;  // 2 ^ 16 = 65536
    vector<vector<int>> ancestors;
public:
    TreeAncestor(int n, vector<int>& parent) {
        ancestors = vector<vector<int>>(n, vector<int>(Log, -1));
        for (int i = 0; i < n; i++) {
            ancestors[i][0] = parent[i];
        }
        for (int j = 1; j < Log; j++) {
            for (int i = 0; i < n; i++) {
                if (ancestors[i][j - 1] != -1) {  // don't forget
                    ancestors[i][j] = ancestors[ancestors[i][j - 1]][j - 1];
                }
            }
        }
    }
    
    int getKthAncestor(int node, int k) {
        for (int j = 0; j < Log && node != -1; j++) {
            if ((k >> j) & 1) {
                node = ancestors[node][j];
            }
        }
        return node;
    }
};

Python

# from typing import List


Log = 16

class TreeAncestor:
    def __init__(self, n: int, parent: List[int]):
        self.ancestors = [[parent[i]] + [-1] * (Log - 1) for i in range(n)]
        for j in range(1, Log):
            for i in range(n):
                if self.ancestors[i][j - 1] != -1:
                    self.ancestors[i][j] = self.ancestors[self.ancestors[i][j - 1]][j - 1]

    def getKthAncestor(self, node: int, k: int) -> int:
        for j in range(Log):
            if (k >> j) & 1:
                node = self.ancestors[node][j]
            if node == -1:
                break
        return node

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/137426434