2581.统计可能的树根数目

【LetMeFly】2581.统计可能的树根数目：换根DP(树形DP)

力扣题目链接：https://leetcode.cn/problems/count-number-of-possible-root-nodes/

Alice 有一棵 n 个节点的树，节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示，其中 edges[i] = [ai, bi] ，表示树中节点 ai 和 bi 之间有一条边。

Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测，Bob 做如下事情：

• 选择两个 不相等 的整数 u 和 v ，且树中必须存在边 [u, v] 。
• Bob 猜测树中 u 是 v 的 父节点 。

Bob 的猜测用二维整数数组 guesses 表示，其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。

Alice 非常懒，她不想逐个回答 Bob 的猜测，只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。

给你二维整数数组 edges ，Bob 的所有猜测和整数 k ，请你返回可能成为树根的 节点数目 。如果没有这样的树，则返回 0。

 

示例 1：

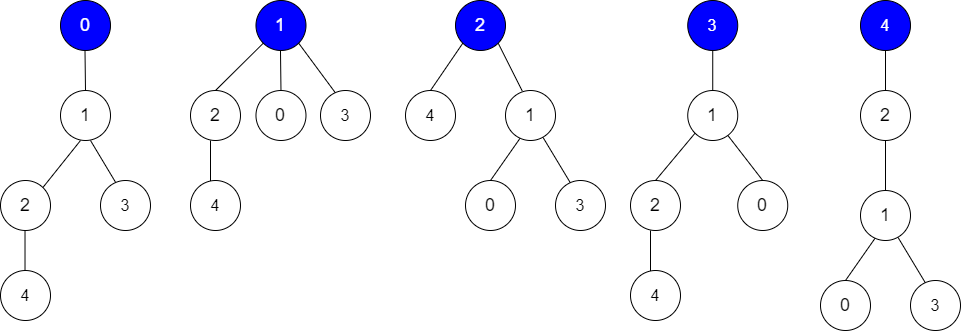
输入：edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出：3
解释：
根为节点 0 ，正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ，正确的猜测为 [1,0], [2,4]
根为节点 4 ，正确的猜测为 [1,3], [1,0]
节点 0 ，1 或 2 为根时，可以得到 3 个正确的猜测。

示例 2：

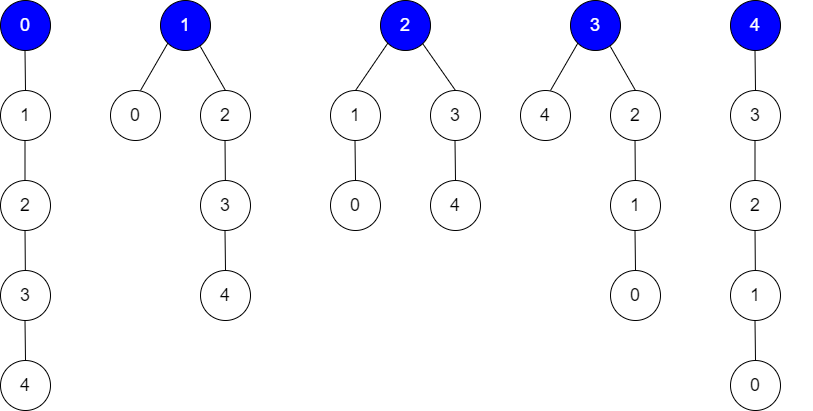
输入：edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出：5
解释：
根为节点 0 ，正确的猜测为 [3,4]
根为节点 1 ，正确的猜测为 [1,0], [3,4]
根为节点 2 ，正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ，正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ，正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根，都至少有 1 个正确的猜测。

 

提示：

• edges.length == n - 1
• 2 <= n <= 105
• 1 <= guesses.length <= 105
• 0 <= ai, bi, uj, vj <= n - 1
• ai != bi
• uj != vj
• edges 表示一棵有效的树。
• guesses[j] 是树中的一条边。
• guesses 是唯一的。
• 0 <= k <= guesses.length

方法一：换根DP(树形DP)

首先我们可以把所有的猜想都存入哈希表中，以便对于某条边，能快速知道其是否有被猜过。

由于节点范围是$10^5$，因此可以将$父节点 \times 10^6 + 子节点$作为哈希表的键值。（注意可能会超32位整数）

假如只问“0”为根的话猜中次数是否$\geq k$，那么我们只需要从$0$开始对树进行深度优先搜索：

搜索过程中统计边被猜中的次数（借助哈希表可以在$O(1)$时间内完成一次查询），搜索结束后判断是否$\geq k$。

现在要问“各个节点”为根的话猜中次数。怎么办？在原有结果的基础上再DP一次即可：

假设在现有的基础上，x是y的父节点。此时有cnt个猜中的边。若把y变成x的父节点呢？

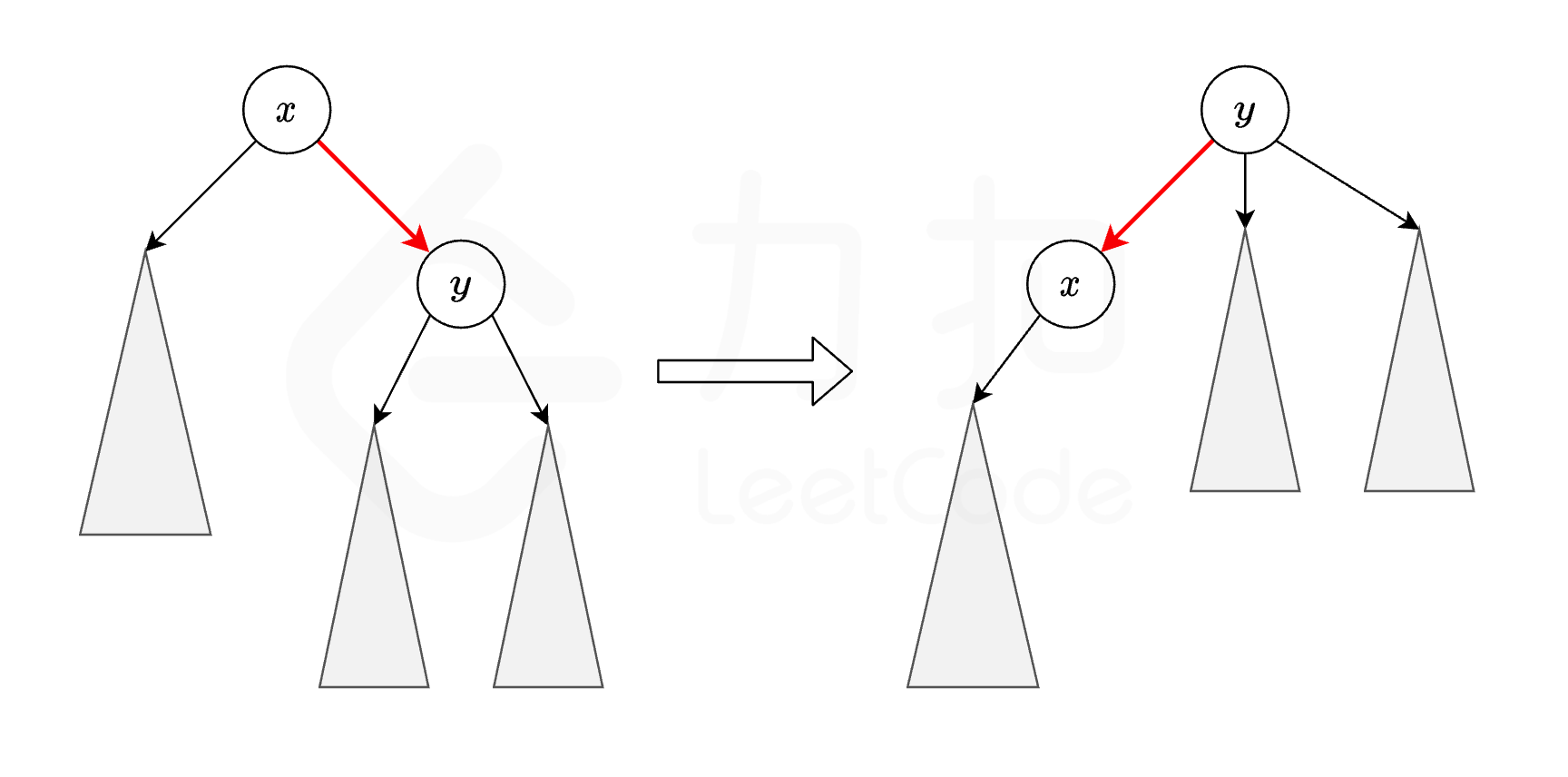
变化的只有x与y之间的一条边。

若有猜(x, y)，则猜中次数$cnt-1$；若有猜(y, x)，则猜中次数$cnt+1$。

DP过程中（其实就是沿边走的过程）不断将父子关系对调，并统计$cnt\geq k$的个数即为答案。

• 时间复杂度$O(N + M)$，其中$N$是树的节点个数，$M=len(guesses)$
• 空间复杂度$O(N+M)$

AC代码

C++

typedef long long ll;
class Solution {
private:
    int cnt;  // 以0为根时答对的数目
    int ans;
    int k;
    vector<vector<int>> graph;
    unordered_set<ll> se;


    void dfs(int thisNode, int lastNode=-1) {
        for (int nextNode : graph[thisNode]) {
            if (nextNode == lastNode) {
                continue;
            }
            if (se.count((ll)thisNode * 1000000 + nextNode)) {
                cnt++;
            }
            dfs(nextNode, thisNode);
        }
    }

    void change(int thisNode, int lastNode, int cnt) {
        int cnt_bak = cnt;
        for (int nextNode : graph[thisNode]) {
            if (nextNode == lastNode) {
                continue;
            }
            if (se.count((ll)thisNode * 1000000 + nextNode)) {
                cnt--;
            }
            if (se.count((ll)nextNode * 1000000 + thisNode)) {
                cnt++;
            }
            ans += cnt >= k;
            change(nextNode, thisNode, cnt);
            cnt = cnt_bak;
        }
    }
public:
    int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
        graph.resize(edges.size() + 1);
        for (vector<int>& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        for (vector<int>& guess : guesses) {
            se.insert((ll)guess[0] * 1000000 + guess[1]);
        }
        cnt = 0;
        this->k = k;
        dfs(0);
        ans = cnt >= k;
        change(0, -1, cnt);
        return ans;
    }
};

Python

from typing import List

class Solution:  # AC,100.00%,92.59%
    def dfs(self, thisNode: int, lastNode: int) -> None:
        for nextNode in self.graph[thisNode]:
            if nextNode == lastNode:
                continue
            if (thisNode * 1000000 + nextNode) in self.se:
                self.cnt += 1
            self.dfs(nextNode, thisNode)
    
    def change(self, thisNode: int, lastNode: int, cnt: int) -> None:
        cnt_bak = cnt
        for nextNode in self.graph[thisNode]:
            if nextNode == lastNode:
                continue
            if (thisNode * 1000000 + nextNode) in self.se:
                cnt -= 1
            if (nextNode * 1000000 + thisNode) in self.se:
                cnt += 1
            self.ans += cnt >= self.k
            self.change(nextNode, thisNode, cnt)
            cnt = cnt_bak            

    def rootCount(self, edges: List[List[int]], guesses: List[List[int]], k: int) -> int:
        self.graph = [[] for _ in range(len(edges) + 1)]
        for x, y in edges:
            self.graph[x].append(y)
            self.graph[y].append(x)
        self.se = set()
        for x, y in guesses:
            self.se.add(x * 1000000 + y)
        self.cnt = 0
        self.dfs(0, -1)
        self.k = k
        self.ans = 1 if self.cnt >= k else 0
        self.change(0, -1, self.cnt)
        return self.ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136372137