1615.最大网络秩

【LetMeFly】1615.最大网络秩

力扣题目链接：https://leetcode.cn/problems/maximal-network-rank/

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算 一次 。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

 

示例 1：

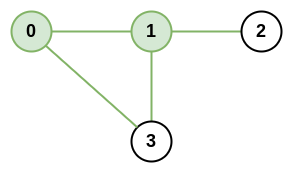
输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出：4
解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

示例 2：

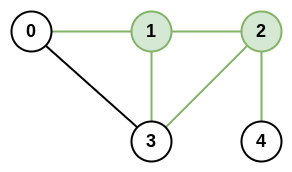
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出：5
解释：共有 5 条道路与城市 1 或 2 相连。

示例 3：

输入：n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出：5
解释：2 和 5 的网络秩为 5，注意并非所有的城市都需要连接起来。

 

提示：

• 2 <= n <= 100
• 0 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 2
• 0 <= ai, bi <= n-1
• ai != bi
• 每对城市之间 最多只有一条 道路相连

方法一：图 + 哈希表

使用一个长度为$n$的整型数组$cnt$，其中$cnt[i]$代表节点$i$相连的路径的数量。

使用一个哈希表$se$记录路径$(i, j)$或路径$(j, i)$是否存在。

初始时遍历所有路径，统计出$cnt$和$se$

接着枚举所有的“城市对”（也就是枚举所有不相同的两个城市），那么这两个城市（记为i和j）之间的“网络秩”就是$cnt[i]+cnt[j]-se.count((i, j))$

• 时间复杂度$O(n^2 + \sum roads)$
• 空间复杂度$O(n + \sum roads)$

AC代码

C++

C++想要使用内置哈希表的话，可以选择将（i * 1000 + j）作为键值存入。

class Solution {
public:
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        int ans = 0;
        vector<int> cnt(n);
        unordered_set<int> se;
        for (vector<int>& road : roads) {
            cnt[road[0]]++;
            cnt[road[1]]++;
            se.insert(road[0] * 1000 + road[1]);
            se.insert(road[1] * 1000 + road[0]);
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                ans = max(ans, cnt[i] + cnt[j] - (int)se.count(i * 1000 + j));
            }
        }
        return ans;
    }
};

Python

# from typing import List

class Solution:
    def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
        ans = 0
        cnt = [0 for _ in range(n)]
        se = set()
        for road in roads:
            cnt[road[0]] += 1
            cnt[road[1]] += 1
            se.add((road[0], road[1]))
            se.add((road[1], road[0]))
        for i in range(n):
            for j in range(i + 1, n):
                ans = max(ans, cnt[i] + cnt[j] - ((i, j) in se))
        return ans

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/129546421