【LetMeFly】1857.有向图中最大颜色值:拓扑排序+动态规划
力扣题目链接:https://leetcode.cn/problems/largest-color-value-in-a-directed-graph/
给你一个 有向图 ,它含有 n 个节点和 m 条边。节点编号从 0 到 n - 1 。
给你一个字符串 colors ,其中 colors[i] 是小写英文字母,表示图中第 i 个节点的 颜色 (下标从 0 开始)。同时给你一个二维数组 edges ,其中 edges[j] = [aj, bj] 表示从节点 aj 到节点 bj 有一条 有向边 。
图中一条有效 路径 是一个点序列 x1 -> x2 -> x3 -> ... -> xk ,对于所有 1 <= i < k ,从 xi 到 xi+1 在图中有一条有向边。路径的 颜色值 是路径中 出现次数最多 颜色的节点数目。
请你返回给定图中有效路径里面的 最大颜色值 。如果图中含有环,请返回 -1 。
示例 1:
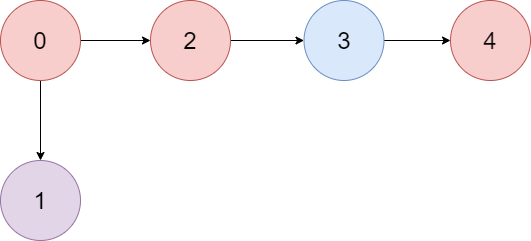
输入:colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
输出:3
解释:路径 0 -> 2 -> 3 -> 4 含有 3 个颜色为 "a" 的节点(上图中的红色节点)。
示例 2:
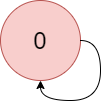
输入:colors = "a", edges = [[0,0]]
输出:-1
解释:从 0 到 0 有一个环。
提示:
n == colors.lengthm == edges.length1 <= n <= 1050 <= m <= 105colors 只含有小写英文字母。0 <= aj, bj < n
解题方法:拓扑排序+动态规划
记录每个节点的入度(入度为指向这个节点的边的个数),记录每个节点指向哪些节点。
创建一个队列,一旦有节点入度为0则入队(拓扑排序)。
创建一个DP数组,DP[i][j]表示从路径起点到节点i颜色j的最大个数。
队列非空时:
每次从队列中取出一个节点(thisNode),DP数组中这个节点自身的颜色值加一。
遍历这个节点指向的所有节点(nextNode),被指向节点入度减一,更新被指向节点的每种颜色最大值dp[nextNode][j]为max(dp[nextNode][j], dp[thisNode][j])。
最终,若仍有节点入度非零,则代表有环,返回-1;否则,返回dp[i][j]中最大的一个。
- 时间复杂度$O((m+n)C)$,其中$C=26$
- 空间复杂度$O(nC+m)$
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public:
int largestPathValue(string colors, vector<vector<int>>& edges) {
vector<vector<int>> out(colors.size());
vector<int> indegree(colors.size());
for (vector<int>& edge: edges) {
out[edge[0]].push_back(edge[1]);
indegree[edge[1]]++;
}
queue<int> q;
for (int i = 0; i < colors.size(); i++) {
if (!indegree[i]) {
q.push(i);
}
}
vector<array<int, 26>> dp(colors.size());
int ans = 0;
while (q.size()) {
int thisNode = q.front();
q.pop();
ans = max(ans, ++dp[thisNode][colors[thisNode] - 'a']);
for (int nextNode : out[thisNode]) {
indegree[nextNode]--;
if (!indegree[nextNode]) {
q.push(nextNode);
}
for (int i = 0; i < 26; i++) {
dp[nextNode][i] = max(dp[nextNode][i], dp[thisNode][i]);
}
}
}
for (int i = 0; i < colors.size(); i++) {
if (indegree[i]) {
return -1;
}
}
return ans;
}
};
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| '''
Author: LetMeFly
Date: 2025-05-26 22:02:44
LastEditors: LetMeFly.xyz
LastEditTime: 2025-05-26 23:34:26
'''
from typing import List
class Solution:
def largestPathValue(self, colors: str, edges: List[List[int]]) -> int:
out = [[] for _ in range(len(colors))]
indegree = [0] * len(colors)
for x, y in edges:
out[x].append(y)
indegree[y] += 1
q = []
for i in range(len(colors)):
if indegree[i] == 0:
q.append(i)
dp = [[0] * 26 for _ in range(len(colors))]
ans = 0
while q:
thisNode = q.pop()
dp[thisNode][ord(colors[thisNode]) - ord('a')] += 1
ans = max(ans, dp[thisNode][ord(colors[thisNode]) - ord('a')])
for nextNode in out[thisNode]:
indegree[nextNode] -= 1
if not indegree[nextNode]:
q.append(nextNode)
for i in range(26):
dp[nextNode][i] = max(dp[nextNode][i], dp[thisNode][i])
if any(indegree):
return -1
return ans
|
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
import java.util.List;
import java.util.ArrayList;
import java.util.Queue;
import java.util.LinkedList;
class Solution {
public int largestPathValue(String colors, int[][] edges) {
List<Integer>[] out = new ArrayList[colors.length()];
for (int i = 0; i < colors.length(); i++) {
out[i] = new ArrayList<>();
}
int[] indegree = new int[colors.length()];
for (int[] edge : edges) {
out[edge[0]].add(edge[1]);
indegree[edge[1]]++;
}
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < colors.length(); i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
int[][]dp = new int[colors.length()][26];
int ans = 0;
while (!q.isEmpty()) {
int thisNode = q.poll();
ans = Math.max(ans, ++dp[thisNode][colors.charAt(thisNode) - 'a']);
for (int nextNode : out[thisNode]) {
indegree[nextNode]--;
if (indegree[nextNode] == 0) {
q.offer(nextNode);
}
for (int i = 0; i < 26; i++) {
dp[nextNode][i] = Math.max(dp[nextNode][i], dp[thisNode][i]);
}
}
}
for (int i = 0; i < colors.length(); i++) {
if (indegree[i] != 0) {
return -1;
}
}
return ans;
}
}
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
package main
func largestPathValue(colors string, edges [][]int) (ans int) {
out := make([][]int, len(colors))
for i := range out {
out[i] = make([]int, 0)
}
indegree := make([]int, len(colors))
for _, edge := range edges {
out[edge[0]] = append(out[edge[0]], edge[1])
indegree[edge[1]]++
}
q := []int{}
for i, v := range indegree {
if v == 0 {
q = append(q, i)
}
}
dp := make([][]int, len(colors))
for i := range dp {
dp[i] = make([]int, 26)
}
for len(q) > 0 {
thisNode := q[len(q) - 1]
q = q[:len(q) - 1]
dp[thisNode][colors[thisNode] - 'a']++
ans = max(ans, dp[thisNode][colors[thisNode] - 'a'])
for _, nextNode := range out[thisNode] {
indegree[nextNode]--
if indegree[nextNode] == 0 {
q = append(q, nextNode)
}
for i := 0; i < 26; i++ {
dp[nextNode][i] = max(dp[nextNode][i], dp[thisNode][i])
}
}
}
for _, v := range indegree {
if v != 0 {
return -1
}
}
return
}
|
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
千篇源码题解已开源

