【LetMeFly】1931.用三种不同颜色为网格涂色(PLUS):动态规划/矩阵快速幂 - n=10^18也能做
力扣题目链接:https://leetcode.cn/problems/painting-a-grid-with-three-different-colors/
给你两个整数 m 和 n 。构造一个 m x n 的网格,其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。
涂色方案需要满足:不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大, 返回 对 109 + 7 取余 的结果。
示例 1:

输入:m = 1, n = 1
输出:3
解释:如上图所示,存在三种可能的涂色方案。
示例 2:
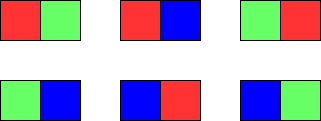
输入:m = 1, n = 2
输出:6
解释:如上图所示,存在六种可能的涂色方案。
示例 3:
输入:m = 5, n = 5
输出:580986
提示:
1 <= m <= 51 <= n <= 1000
解题方法一:动态规划
解题思路
有没有发现这道题$m$很小,发现的话就很容易想到一列最多有$3^m$种可能。
诶,那解法不就来了?
我首先枚举第一列的所有可行情况,再枚举第二列的所有可行情况
假设$m=2$,第一列为“蓝白”的话,第二列可以为“白蓝”、“白红”或“红蓝”。
假设第一列为“蓝白”的方案数一共有1种,那么第二列为“白蓝”、“白红”、“红蓝”的方案数分别加$1$。
第一列为“蓝红”的话(假设方案数为$t$),第二列为“白蓝”、“红白”、“红蓝”的方案数分别加$t$。
总之,知道了前一列每种摆放方式的方案数,就能知道后一列每种摆放方式的方案数了。
具体方法
如何表示“某一列的方案”
一列的方案数不超过$3^m$,使用一个整数表示即可。
整数范围是$0$到$3^m-1$,整数$code$的$\lceil\frac{code}{3^{m-1}}\rceil%3$代表这一列第$m$个ceil的颜色是$0$还是$1$还是$2$。
如何判断某一列的方案是否合法
看这一列相邻两个格子是否相同。
如何判断合法的两列能否相邻
看这两列的$m$行中是否有一行颜色相同。
具体点
具体来说,我们可以建立一个“映射”okList,$okList[i][j]$表示$i$可以和$j$相邻。
假设一列的可行方案数实际有$ok1type$种,也可以创建一个长度为$ok1type$的数组$firstCol$代表这一列每种摆放方式的方案数;
使用一个哈希表将某一列的方案编码$code$映射为$firstCol$的下标,使用一个哈希表将$firstCol$的下标映射为某一列的方案编码$code$。
这样,就能依据三个哈希表,由上一列每种摆放方式的方案数推算出下一列每种摆放方式的方案数了。
时空复杂度分析
- 时间复杂度$O(m\times 3^{2m}+n\times 3^{2m})$
- 空间复杂度$O(3^{2m})$
别看$3^{2m}$似乎不小,但其实即使$m=5$,一列的可行方案数也只有48。
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
class Solution {
private:
static constexpr int pow[6] = {1, 3, 9, 27, 81, 243};
static constexpr int MOD = 1e9 + 7;
inline int getTh(int a, int n) {
return a / pow[n] % 3;
}
bool ok(int a, int b, int m) {
if (a % 3 == b % 3) {
return false;
}
for (int i = 1; i < m; i++) {
if (getTh(a, i) == getTh(b, i) || getTh(a, i) == getTh(a, i - 1) || getTh(b, i) == getTh(b, i - 1)) {
return false;
}
}
return true;
}
public:
int colorTheGrid(int m, int n) {
int types = pow[m];
unordered_map<int, vector<int>> okList;
for (int i = 0; i < types; i++) {
for (int j = 0; j < types; j++) {
if (ok(i, j, m)) {
okList[i].push_back(j);
}
}
}
int ok1type = okList.size();
vector<int> firstCol(ok1type, 1), secondCol(ok1type);
unordered_map<int, int> code2idx(ok1type);
unordered_map<int, int> idx2code(ok1type);
int th = 0;
for (unordered_map<int, vector<int>>::iterator it = okList.begin(); it != okList.end(); it++, th++) {
code2idx[it->first] = th;
idx2code[th] = it->first;
}
for (int j = 2; j <= n; j++) {
for (int t = 0; t < ok1type; t++) {
int lastCode = idx2code[t];
for (int nextCode : okList[lastCode]) {
secondCol[code2idx[nextCode]] = (secondCol[code2idx[nextCode]] + firstCol[t]) % MOD;
}
}
firstCol = move(secondCol);
secondCol = vector<int>(ok1type);
}
int ans = 0;
for (int t : firstCol) {
ans = (ans + t) % MOD;
}
return ans;
}
};
|
解题方法二:矩阵快速幂
我们将前一列每种可行摆放方法的方案数记为$F={f_0, f_1, …}^T$,将后一列的方案数记为$S={s_0, s_1, …}^T$
那么其实$S$可以由一个矩阵(记为$M$)乘上$F$得到。
假设摆放方法$0$可以和$1, 2$相邻,$1$可以和$1, 3$相邻(现实情况中当然不可能),则有:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| firstCol:
[
f0
f1
f2
f3
]
mapping:
0: {1, 2}
1: {1, 3}
2: {}
3: {}
secondCol:
[
s0=0
s1=f0+f1
s2=f0
s3=f1
]
matrix
[ [ [
s0=0 [0 0 0 0] f0
s1=f0+f1 -- [1 1 0 0] \/ f1
s2=f0 -- [1 0 0 0] /\ f2
s3=f1 [0 1 0 0] f3
] ] ]
S = M×F
|
其中若方案$i$的下一列可以是方案$j$则$M[j][i]=1$。
一共$n$列,一共左乘$n-1$次$M$,最终结果$S=M^{n-1}F$,其中初始值第一列$F$的每一个元素都是$1$。
而矩阵快速幂的方法和快速幂是一样的。
- 时间复杂度$O(3^{2m}\log n)$
- 空间复杂度$O(3^{2m})$
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
|
typedef long long ll;
typedef vector<vector<int>> matrix;
class Solution {
private:
int singleNum;
static constexpr int MOD = 1e9 + 7;
static constexpr int pow[6] = {1, 3, 9, 27, 81, 243};
inline int getTh(int a, int n) {
return a / pow[n] % 3;
}
inline bool isOk(int a, int m) {
for (int i = 1; i < m; i++) {
if (getTh(a, i) == getTh(a, i - 1)) {
return false;
}
}
return true;
}
inline bool isOk(int a, int b, int m) {
for (int i = 0; i < m; i++) {
if (getTh(a, i) == getTh(b, i)) {
return false;
}
}
return true;
}
matrix mul(matrix a, matrix b) {
matrix ans(singleNum, vector<int>(singleNum));
for (int i = 0; i < singleNum; i++) {
for (int k = 0; k < singleNum; k++) {
for (int j = 0; j < singleNum; j++) {
ans[i][j] = (ans[i][j] + (ll)a[i][k] * b[k][j] % MOD) % MOD;
}
}
}
return ans;
}
matrix Pow(matrix a, int b) {
matrix ans(singleNum, vector<int>(singleNum));
for (int i = 0; i < singleNum; i++) {
ans[i][i] = 1;
}
while (b) {
if (b & 1) {
ans = mul(ans, a);
}
a = mul(a, a);
b >>= 1;
}
return ans;
}
public:
int colorTheGrid(int m, int n) {
vector<int> singleOk;
for (int i = 0; i < pow[m]; i++) {
if (isOk(i, m)) {
singleOk.push_back(i);
}
}
singleNum = singleOk.size();
matrix M(singleNum, vector<int>(singleNum));
for (int i = 0; i < singleNum; i++) {
for (int j = 0; j < singleNum; j++) {
if (isOk(singleOk[i], singleOk[j], m)) {
M[j][i] = 1;
}
}
}
matrix Mn = Pow(M, n - 1);
int ans = 0;
for (int i = 0; i < singleNum; i++) {
for (int j = 0; j < singleNum; j++) {
ans = (ans + Mn[i][j]) % MOD;
}
}
return ans;
}
};
|
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
千篇源码题解已开源

