【LetMeFly】2360.图中的最长环:一步一打卡(不撞南墙不回头) - 通过故事讲道理
力扣题目链接:https://leetcode.cn/problems/longest-cycle-in-a-graph/
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,其中每个节点 至多 有一条出边。
图用一个大小为 n 下标从 0 开始的数组 edges 表示,节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边,那么 edges[i] == -1 。
请你返回图中的 最长 环,如果没有任何环,请返回 -1 。
一个环指的是起点和终点是 同一个 节点的路径。
示例 1:
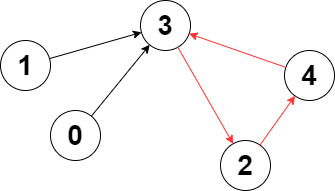
输入:edges = [3,3,4,2,3]
输出去:3
解释:图中的最长环是:2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ,所以返回 3 。
示例 2:
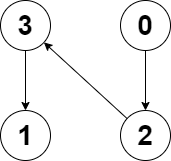
输入:edges = [2,-1,3,1]
输出:-1
解释:图中没有任何环。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
解题方法:一步一打卡(不撞南墙不回头)
故事
小T爱跑图,她有如下爱好:
- 只跑没跑到过的景点
- 不撞南墙不回头(一直跑下去,直到跑到一个跑到过的景点)
- 爱打卡(第一次跑到一个景点,就打卡记录下“这是我解锁的第xx个城市”)
小T跑完所有景点,这道题就解决了。
原理解析
这得益于每个景点最多只有一个“下一个景点”(每个节点至多有一条出边)。
具体实现
使用一个$visited$数组记录一下每个景点的打卡记录,使用$cnt$记录即将要解锁的城市是第几个。
从任意一点开始尝试,按照小T的跑法开始模拟,遇到新城市就打卡记录并尝试继续,直到到达终点或遇到了去过的城市为止。
小T停止这条路线后:
- 如果停止位置指向下一个城市($edges[i]\neq -1$),则说明是到达了去过的城市(而不是达到了单链的终点)
- 并且如果该城市的打卡记录不早于本次路线的开始时间,则说明是本次跑步过程中遇到的城市,说明有环
什么意思呢?小T开始一条新的路线时,还需要记录一下新路线开始时一共打卡了多少城市。
遇到了一个去过城市,如果打卡记录编号很小(不是本次路线上遇到的,而是之前经过的),就不能说明有环。
反之,如果这个去过的城市是本次线路上二次遇到的,就说明有环。
时空复杂度分析
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
class Solution {
public:
int longestCycle(vector<int>& edges) {
int ans = -1;
int cnt = 1;
vector<int> visited(edges.size());
for (int i = 0; i < edges.size(); i++) {
int begin = cnt, x = i;
while (edges[x] != -1 && !visited[x]) {
visited[x] = cnt++;
x = edges[x];
}
if (edges[x] != -1 && visited[x] >= begin) {
ans = max(ans, cnt - visited[x]);
}
}
return ans;
}
};
#ifdef _WIN32
int main() {
string s;
while (cin >> s) {
vector<int> v = stringToVector(s);
Solution sol;
cout << sol.longestCycle(v) << endl;
}
return 0;
}
#endif
|
Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| '''
Author: LetMeFly
Date: 2025-03-29 14:06:24
LastEditors: LetMeFly.xyz
LastEditTime: 2025-03-29 14:09:27
'''
from typing import List
class Solution:
def longestCycle(self, edges: List[int]) -> int:
ans = -1
cnt = 1
visited = [0] * len(edges)
for i in range(len(edges)):
begin = cnt
while edges[i] != -1 and not visited[i]:
visited[i] = cnt
cnt += 1
i = edges[i]
if edges[i] != -1 and visited[i] >= begin:
ans = max(ans, cnt - visited[i])
return ans
|
Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public int longestCycle(int[] edges) {
int ans = -1;
int cnt = 1;
int[] visited = new int[edges.length];
for (int i = 0; i < edges.length; i++) {
int begin = cnt;
int x = i;
while (edges[x] != -1 && visited[x] == 0) {
visited[x] = cnt++;
x = edges[x];
}
if (edges[x] != -1 && visited[x] >= begin) {
ans = Math.max(ans, cnt - visited[x]);
}
}
return ans;
}
}
|
Go
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
package main
func longestCycle(edges []int) int {
ans := -1
cnt := 1
visited := make([]int, len(edges))
for i := range edges {
begin := cnt
for edges[i] != -1 && visited[i] == 0 {
visited[i] = cnt
cnt++
i = edges[i]
}
if edges[i] != -1 && visited[i] >= begin {
ans = max(ans, cnt - visited[i])
}
}
return ans
}
|
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
千篇源码题解已开源

