3218.切蛋糕的最小总开销 I

【LetMeFly】3218.切蛋糕的最小总开销 I：记忆化搜索(深度优先搜索DFS)

力扣题目链接：https://leetcode.cn/problems/minimum-cost-for-cutting-cake-i/

有一个 m x n 大小的矩形蛋糕，需要切成 1 x 1 的小块。

给你整数 m ，n 和两个数组：

  • horizontalCut 的大小为 m - 1 ，其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
  • verticalCut 的大小为 n - 1 ，其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。

一次操作中，你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一：

  1. 沿着水平线 i 切开蛋糕，开销为 horizontalCut[i] 。
  2. 沿着垂直线 j 切开蛋糕，开销为 verticalCut[j] 。

每次操作后，这块蛋糕都被切成两个独立的小蛋糕。

每次操作的开销都为最开始对应切割线的开销，并且不会改变。

请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。

 

示例 1：

输入：m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

输出：13

解释：

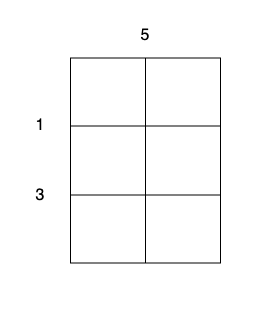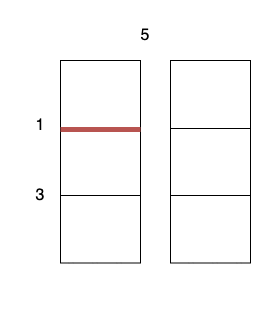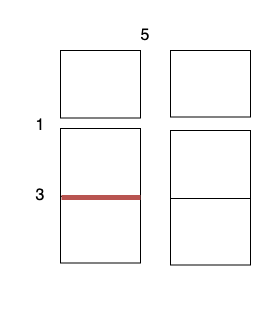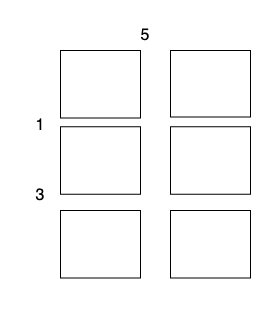
  • 沿着垂直线 0 切开蛋糕，开销为 5 。
  • 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
  • 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
  • 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。
  • 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。

总开销为 5 + 1 + 1 + 3 + 3 = 13 。

示例 2：

输入：m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

输出：15

解释：

  • 沿着水平线 0 切开蛋糕，开销为 7 。
  • 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。
  • 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。

总开销为 7 + 4 + 4 = 15 。

 

提示：

  • 1 <= m, n <= 20
  • horizontalCut.length == m - 1
  • verticalCut.length == n - 1
  • 1 <= horizontalCut[i], verticalCut[i] <= 103

解题方法：深度优先搜索（记忆化）

写一个函数dfs计算：切割竖直方向[ia, ib)水平方向[ja, jb)这个子蛋糕所需的最小花费。

每次计算很简单，若已经是1x1大小则直接返回0，若是水平切割：

枚举所有水平切割的下刀位置。其中，递归计算上下两块新蛋糕所需的最小花费并加上这一刀的花费作为这种切割方法的最小花费。

若是竖直切割则同理。

直接使用整块大蛋糕的大小调用dfs函数即可求得答案。

  • 时间复杂度$O(m^2n^2(m+n))$。共有$m^2n^2$种子蛋糕方案，每种方案首次计算平均耗时$O(m+n)$。
  • 空间复杂度$O(m^2n^2)$

AC代码

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
 * @Author: LetMeFly
 * @Date: 2024-12-25 18:08:17
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-25 18:40:56
 */
class Solution {
private:
    unordered_map<int, int> ma;

    int dfs(int ia, int ib, int ja, int jb, vector<int>& h, vector<int>& v) {
        int code = ia + ib * 20 + ja * 400 + jb * 8000;
        if (ma.count(code)) {
            return ma[code];
        }
        int ans = 1000000000;
        if (ib - ia == 1 && jb - ja == 1) {
            ans = 0;
        }
        for (int ic = ia + 1; ic < ib; ic++) {
            ans = min(ans, h[ic - 1] + dfs(ia, ic, ja, jb, h, v) + dfs(ic, ib, ja, jb, h, v));
        }
        for (int jc = ja + 1; jc < jb; jc++) {
            ans = min(ans, v[jc - 1] + dfs(ia, ib, ja, jc, h, v) + dfs(ia, ib, jc, jb, h, v));
        }
        return ma[code] = ans;
    }
public:
    int minimumCost(int m, int n, vector<int>& horizontalCut, vector<int>& verticalCut) {
        return dfs(0, m, 0, n, horizontalCut, verticalCut);
    }
};

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
'''
Author: LetMeFly
Date: 2024-12-25 20:27:10
LastEditors: LetMeFly.xyz
LastEditTime: 2024-12-25 20:34:17
'''
from typing import List
from functools import cache

class Solution:
    @cache
    def dfs(self, ia: int, ib: int, ja: int, jb: int) -> int:
        if ib - ia == 1 and jb - ja == 1:
            return 0
        ans = 1000000000
        for ic in range(ia + 1, ib):
            ans = min(ans, self.h[ic - 1] + self.dfs(ia, ic, ja, jb) + self.dfs(ic, ib, ja, jb))
        for jc in range(ja + 1, jb):
            ans = min(ans, self.v[jc - 1] + self.dfs(ia, ib, ja, jc) + self.dfs(ia, ib, jc, jb))
        return ans

    def minimumCost(self, m: int, n: int, horizontalCut: List[int], verticalCut: List[int]) -> int:
        self.h, self.v = horizontalCut, verticalCut
        return self.dfs(0, m, 0, n)

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
 * @Author: LetMeFly
 * @Date: 2024-12-25 20:36:16
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-25 20:42:05
 */
class Solution {
    int[][][][] cache;
    int[] h, v;

    private int dfs(int ia, int ib, int ja, int jb) {
        if (cache[ia][ib][ja][jb] > 0 || (ib == ia + 1 && jb == ja + 1)) {
            return cache[ia][ib][ja][jb];
        }
        int ans = 1000000000;
        for (int ic = ia + 1; ic < ib; ic++) {
            ans = Math.min(ans, h[ic - 1] + dfs(ia, ic, ja, jb) + dfs(ic, ib, ja, jb));
        }
        for (int jc = ja + 1; jc < jb; jc++) {
            ans = Math.min(ans, v[jc - 1] + dfs(ia, ib, ja, jc) + dfs(ia, ib, jc, jb));
        }
        cache[ia][ib][ja][jb] = ans;
        return ans;
    }

    public int minimumCost(int m, int n, int[] horizontalCut, int[] verticalCut) {
        cache = new int[m][m + 1][n][n + 1];
        h = horizontalCut;
        v = verticalCut;
        return dfs(0, m, 0, n);
    }
}

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
 * @Author: LetMeFly
 * @Date: 2024-12-25 20:44:03
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-25 20:56:44
 */
package main

func min_CFCC(a, b int) int {
    if a <= b {
        return a
    }
    return b
}

func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) int {
    cache := make([][][][]int, m)  // [m][m + 1][n][n + 1]
    for i := range cache {
        cache[i] = make([][][]int, m + 1)
        for j := range cache[i] {
            cache[i][j] = make([][]int, n)
            for k := range cache[i][j] {
                cache[i][j][k] = make([]int, n + 1)
            }
        }
    }
    var dfs func(int, int, int, int) int
    dfs = func(ia, ib, ja, jb int) int {
        if cache[ia][ib][ja][jb] > 0 || (ia == ib - 1 && ja == jb - 1) {
            return cache[ia][ib][ja][jb]
        }
        ans := 1000000000
        for ic := ia + 1; ic < ib; ic++ {
            ans = min_CFCC(ans, horizontalCut[ic - 1] + dfs(ia, ic, ja, jb) + dfs(ic, ib, ja, jb))
        }
        for jc := ja + 1; jc < jb; jc++ {
            ans = min_CFCC(ans, verticalCut[jc - 1] + dfs(ia, ib, ja, jc) + dfs(ia, ib, jc, jb))
        }
        cache[ia][ib][ja][jb] = ans
        return ans
    }
    return dfs(0, m, 0, n)
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/144728332

#题解 #中等 #数组 #动态规划 #贪心 #排序 #LeetCode #记忆化搜索 #深度优先搜索 #DFS
3218.切蛋糕的最小总开销 I
https://blog.letmefly.xyz/2024/12/25/LeetCode 3218.切蛋糕的最小总开销I/
作者
Tisfy
发布于
2024年12月25日
许可协议