3249.统计好节点的数目

【LetMeFly】3249.统计好节点的数目：深度优先搜索(DFS)

力扣题目链接：https://leetcode.cn/problems/count-the-number-of-good-nodes/

现有一棵 无向 树，树中包含 n 个节点，按从 0 到 n - 1 标记。树的根节点是节点 0 。给你一个长度为 n - 1 的二维整数数组 edges，其中 edges[i] = [ai, bi] 表示树中节点 ai 与节点 bi 之间存在一条边。

如果一个节点的所有子节点为根的 子树 包含的节点数相同，则认为该节点是一个 好节点。

返回给定树中 好节点 的数量。

子树 指的是一个节点以及它所有后代节点构成的一棵树。

 

 

示例 1：

输入：edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]

输出：7

说明：

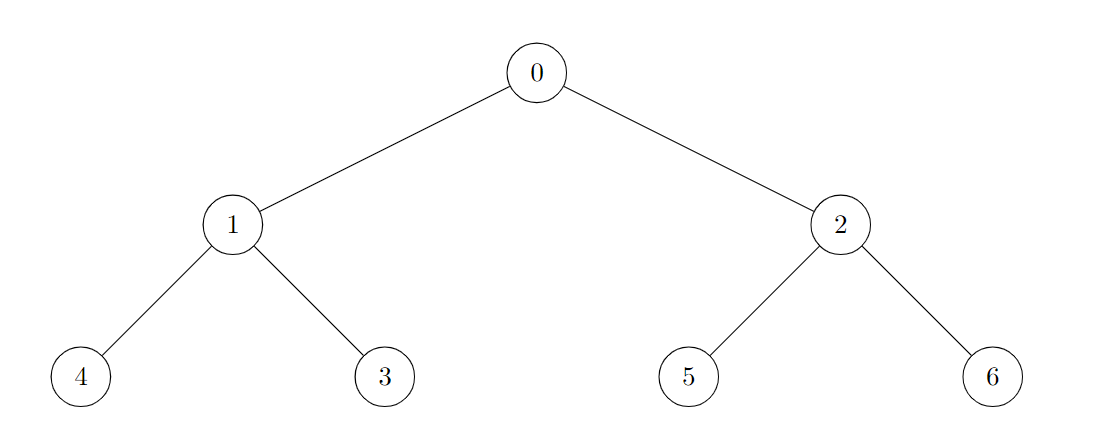
树的所有节点都是好节点。

示例 2：

输入：edges = [[0,1],[1,2],[2,3],[3,4],[0,5],[1,6],[2,7],[3,8]]

输出：6

说明：

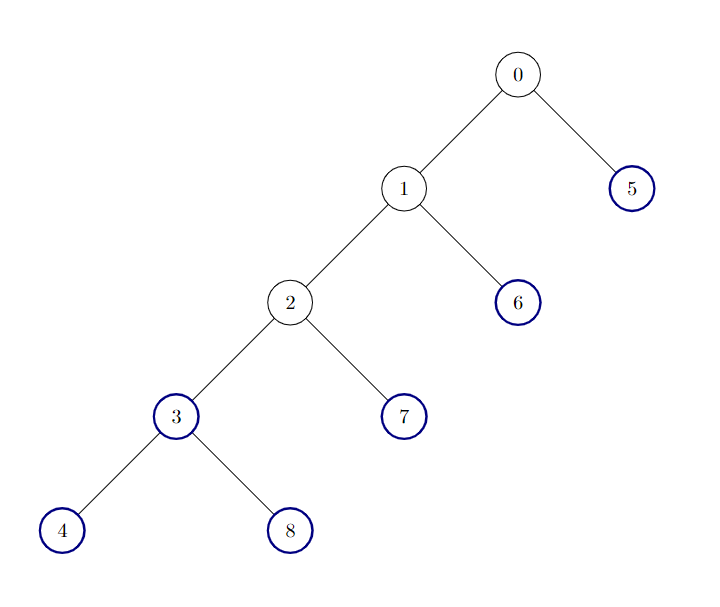
树中有 6 个好节点。上图中已将这些节点着色。

示例 3：

输入：edges = [[0,1],[1,2],[1,3],[1,4],[0,5],[5,6],[6,7],[7,8],[0,9],[9,10],[9,12],[10,11]]

输出：12

解释：

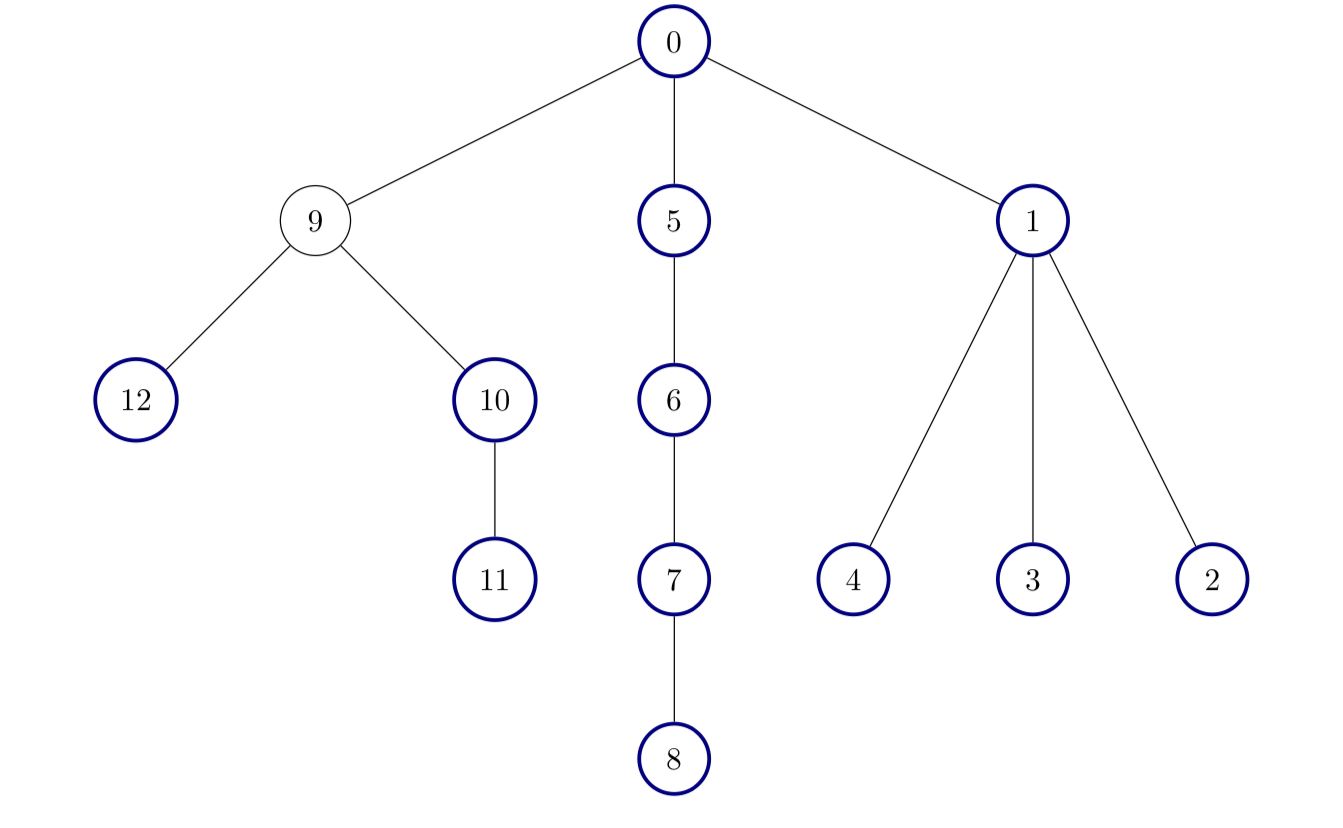
除了节点 9 以外其他所有节点都是好节点。

 

提示：

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• 输入确保 edges 总表示一棵有效的树。

解题方法：深度优先搜索

首先通过“边”建“树”，创建一个graph二维数组，其中graph[x]为所有与x相邻的节点。

接着写一个函数dfs(当前节点, 父节点)，如果当前节点的所有子树大小dfs(子节点)相同，就将全局答案加一。最终返回当前节点为根的子树的大小。

• 时间复杂度$O(n)$，每个节点之后被dfs一次
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
private:
    int ans;
    vector<vector<int>> graph;

    int dfs(int root, int parent=-1) {
        int cnt = 1;
        int oneChild = 0;
        bool thisNodeOk = true;
        for (int nextNode : graph[root]) {
            if (nextNode == parent) {
                continue;
            }
            int nextCnt = dfs(nextNode, root);
            cnt += nextCnt;
            if (oneChild && nextCnt != oneChild) {
                thisNodeOk = false;
            }
            oneChild = nextCnt;
        }
        if (thisNodeOk) {
            ans++;
        }
        return cnt;
    }
public:
    int countGoodNodes(vector<vector<int>>& edges) {
        ans = 0;
        graph.resize(edges.size() + 1);
        for (vector<int>& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        dfs(0);
        return ans;
    }
};

Python

from typing import List

class Solution:
    def dfs(self, thisNode: int, parentNode: int=-1) -> int:
        cnt, oneChild, ok = 1, 0, True
        for nextNode in self.graph[thisNode]:
            if nextNode == parentNode:
                continue
            nextChild = self.dfs(nextNode, thisNode)
            cnt += nextChild
            if not oneChild:
                oneChild = nextChild
            elif oneChild != nextChild:
                ok = False
        if ok:
            self.ans += 1
        return cnt
    
    def countGoodNodes(self, edges: List[List[int]]) -> int:
        self.graph = [[] for _ in range(len(edges) + 1)]
        for x, y in edges:
            self.graph[x].append(y)
            self.graph[y].append(x)
        self.ans = 0
        self.dfs(0)
        return self.ans

Java

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

class Solution {
    private List<Integer>[] graph;
    private int ans;

    private int dfs(int thisNode, int lastNode) {
        int cnt = 1;
        int oneChild = 0;
        boolean ok = true;
        for (int nextChilld : graph[thisNode]) {
            if (nextChilld == lastNode) {
                continue;
            }
            int thisChild = dfs(nextChilld, thisNode);
            cnt += thisChild;
            if (oneChild == 0) {
                oneChild = thisChild;
            } else if (oneChild != thisChild) {
                ok = false;
            }
        }
        if (ok) {
            ans++;
        }
        return cnt;
    }

    public int countGoodNodes(int[][] edges) {
        ans = 0;
        graph = new ArrayList[edges.length + 1];
        Arrays.setAll(graph, i -> new ArrayList<>());
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
            graph[edge[1]].add(edge[0]);
        }
        dfs(0, -1);
        return ans;
    }
}

Go

package main

// import "fmt"

func countGoodNodes(edges [][]int) (ans int) {
    graph := make([][]int, len(edges) + 1)
    for _, edge := range edges {
        graph[edge[0]] = append(graph[edge[0]], edge[1])
        graph[edge[1]] = append(graph[edge[1]], edge[0])
    }
    var dfs func(int, int) int
    dfs = func(thisNode, lastNode int) int {
        // fmt.Println(thisNode, lastNode)
        cnt, oneChild, ok := 1, 0, true
        for _, nextNode := range graph[thisNode] {
            if nextNode == lastNode {
                continue
            }
            thisChild := dfs(nextNode, thisNode)
            cnt += thisChild
            if oneChild == 0 {
                oneChild = thisChild
            } else if oneChild != thisChild {
                ok = false
            }
        }
        if ok {
            ans++
        }
        return cnt
    }
    dfs(0, -1)
    return ans
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/143768804

BTW: 力扣昨天(2024.11.14)上午可以显示在线人员数量了（正在做这道题的人数）