1928.规定时间内到达终点的最小花费

【LetMeFly】1928.规定时间内到达终点的最小花费：动态规划

力扣题目链接：https://leetcode.cn/problems/minimum-cost-to-reach-destination-in-time/

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

 

示例 1：

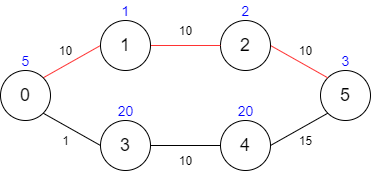
输入：maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：11
解释：最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。

示例 2：

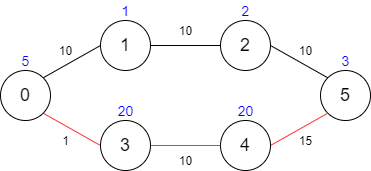
输入：maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：48
解释：最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。

示例 3：

输入：maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：-1
解释：无法在 25 分钟以内从城市 0 到达城市 5 。

 

提示：

• 1 <= maxTime <= 1000
• n == passingFees.length
• 2 <= n <= 1000
• n - 1 <= edges.length <= 1000
• 0 <= xi, yi <= n - 1
• 1 <= timei <= 1000
• 1 <= passingFees[j] <= 1000 
• 图中两个节点之间可能有多条路径。
• 图中不含有自环。

解题方法：动态规划

使用dp[t][i]表示在时间t到达城市i所需最小花费。初始值除了dp[0][0] = passingFees[0]外其余dp[t][i]全为“无穷大”10^7。

对于当前时间t，枚举每一条边（假设这条边连接i和j而花费是cost），若cost <= t，则能更新dp[t][j] = min(dp[t][j], dp[t - cost][i] + passingFees)，dp[t][i]同理。

最终，对于所有的t，dp[t][n - 1]最小的那个即为最小耗时（若为“无穷大”则返回-1）。

• 时间复杂度$O((n+m)\times maxTime)$。其中$n$是节点数，$m$是边数；构建dp数组耗时$O(n\times maxTime)$，动态规划耗时$O(m\times maxTime)$
• 空间复杂度$O(n\times maxTime)$

AC代码

C++

class Solution {
public:
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
        // vector<vector<pair<int, int>>> graph(passingFees.size());
        // for (vector<int>& edge : edges) {
        //     graph[edge[0]].push_back({edge[1], edge[2]});
        //     graph[edge[1]].push_back({edge[0], edge[2]});
        // }
        vector<vector<int>> dp(maxTime + 1, vector<int>(passingFees.size(), 10000000));
        dp[0][0] = passingFees[0];
        for (int t = 1; t <= maxTime; t++) {
            for (vector<int>& edge : edges) {
                int i = edge[0], j = edge[1], thisTime = edge[2];
                if (thisTime <= t) {
                    dp[t][j] = min(dp[t][j], dp[t - thisTime][i] + passingFees[j]);
                    dp[t][i] = min(dp[t][i], dp[t - thisTime][j] + passingFees[i]);
                }
            }
        }
        int ans = 10000000;
        for (int t = 0; t <= maxTime; t++) {
            ans = min(ans, dp[t].back());
        }
        return ans == 10000000 ? -1 : ans;
    }
};

Go

package main

func min(a int, b int) int {
    if a <= b {
        return a
    }
    return b
}

func minCost(maxTime int, edges [][]int, passingFees []int) int {
    dp := make([][]int, maxTime + 1)
    // for _, d := range dp {
    //     d = make([]int, len(passingFees))
    //     for i := range d {
    //         d[i] = 10000000
    //     }
    // }
    for th := range dp {
        dp[th] = make([]int, len(passingFees))
        for i := range dp[th] {
            dp[th][i] = 10000000
        }
    }
    dp[0][0] = passingFees[0]
    
    for t := 1; t <= maxTime; t++ {
        for _, edge := range edges {
            i, j, cost := edge[0], edge[1], edge[2]
            if cost <= t {
                dp[t][j] = min(dp[t][j], dp[t - cost][i] + passingFees[j])
                dp[t][i] = min(dp[t][i], dp[t - cost][j] + passingFees[i])
            }
        }
    }

    ans := 10000000
    for _, d := range dp {
        ans = min(ans, d[len(passingFees) - 1])
    }
    if ans == 10000000 {
        return -1
    }
    return ans
}

Java

import java.util.Arrays;
class Solution {
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        int[][] dp = new int[maxTime + 1][passingFees.length];
        for (int i = 0; i <= maxTime; i++) {
            Arrays.fill(dp[i], 10000000);
        }
        dp[0][0] = passingFees[0];
        for (int t = 1; t <= maxTime; t++) {
            for (int[] edge : edges) {
                int i = edge[0], j = edge[1], cost = edge[2];
                if (cost <= t) {
                    dp[t][j] = Math.min(dp[t][j], dp[t - cost][i] + passingFees[j]);
                    dp[t][i] = Math.min(dp[t][i], dp[t - cost][j] + passingFees[i]);
                }
            }
        }
        int ans = 10000000;
        for (int[] d : dp) {
            ans = Math.min(ans, d[passingFees.length - 1]);
        }
        return ans == 10000000 ? -1 : ans;
    }
}

Python

from typing import List

class Solution:
    def minCost(self, maxTime: int, edges: List[List[int]], passingFees: List[int]) -> int:
        dp = [[10000000] * len(passingFees) for _ in range(maxTime + 1)]
        dp[0][0] = passingFees[0]
        for t in range(1, maxTime + 1):
            for i, j, thisTime in edges:
                if thisTime <= t:
                    dp[t][j] = min(dp[t][j], dp[t - thisTime][i] + passingFees[j])
                    dp[t][i] = min(dp[t][i], dp[t - thisTime][j] + passingFees[i])
        ans = min(d[-1] for d in dp)
        return -1 if ans == 10000000 else ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/142691241