2065.最大化一张图中的路径价值

【LetMeFly】2065.最大化一张图中的路径价值：回溯

力扣题目链接：https://leetcode.cn/problems/maximum-path-quality-of-a-graph/

给你一张 无向 图，图中有 n 个节点，节点编号从 0 到 n - 1 （都包括）。同时给你一个下标从 0 开始的整数数组 values ，其中 values[i] 是第 i 个节点的 价值 。同时给你一个下标从 0 开始的二维整数数组 edges ，其中 edges[j] = [uj, vj, timej] 表示节点 uj 和 vj 之间有一条需要 timej 秒才能通过的无向边。最后，给你一个整数 maxTime 。

合法路径 指的是图中任意一条从节点 0 开始，最终回到节点 0 ，且花费的总时间 不超过 maxTime 秒的一条路径。你可以访问一个节点任意次。一条合法路径的 价值 定义为路径中 不同节点 的价值 之和 （每个节点的价值 至多 算入价值总和中一次）。

请你返回一条合法路径的 最大 价值。

注意：每个节点 至多 有 四条 边与之相连。

 

示例 1：

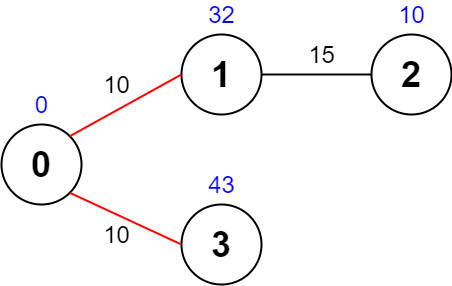
输入：values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
输出：75
解释：
一条可能的路径为：0 -> 1 -> 0 -> 3 -> 0 。总花费时间为 10 + 10 + 10 + 10 = 40 <= 49 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 0 + 32 + 43 = 75 。

示例 2：

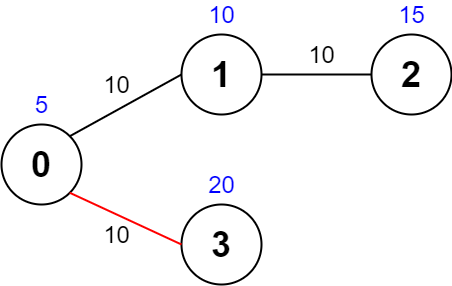
输入：values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
输出：25
解释：
一条可能的路径为：0 -> 3 -> 0 。总花费时间为 10 + 10 = 20 <= 30 。
访问过的节点为 0 和 3 ，最大路径价值为 5 + 20 = 25 。

示例 3：

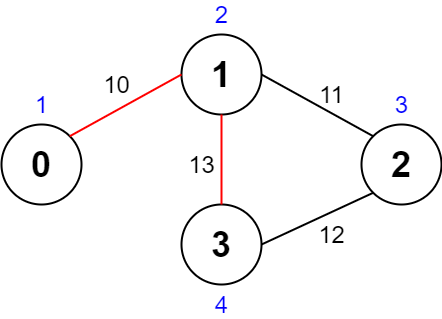
输入：values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
输出：7
解释：
一条可能的路径为：0 -> 1 -> 3 -> 1 -> 0 。总花费时间为 10 + 13 + 13 + 10 = 46 <= 50 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 1 + 2 + 4 = 7 。

示例 4：

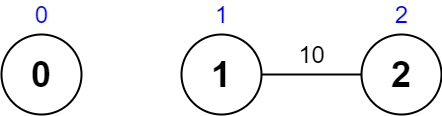
输入：values = [0,1,2], edges = [[1,2,10]], maxTime = 10
输出：0
解释：
唯一一条路径为 0 。总花费时间为 0 。
唯一访问过的节点为 0 ，最大路径价值为 0 。

 

提示：

• n == values.length
• 1 <= n <= 1000
• 0 <= values[i] <= 108
• 0 <= edges.length <= 2000
• edges[j].length == 3
• 0 <= uj < vj <= n - 1
• 10 <= timej, maxTime <= 100
• [uj, vj] 所有节点对 互不相同 。
• 每个节点 至多有四条 边。
• 图可能不连通。

解题方法：回溯

不难发现最大总耗时为100，而单次耗时最少为10。因此最多经过10条边。每个节点最多有4条边相连（说明每走一条边最多有4种选择），因此最多有4^10种行走路线。

写一个函数dfs(int root, int time, int value)用来判断“走到root节点总耗时为time且总价值为value”时的结果：

如果root为0则立刻更新答案；

对于所有与root相邻的节点next，如果“当前时间+路径长度”不超过最大耗时，则：

• 如果走到过next，则递归dfs(next, time + distance, value)（无法再次获得价值）
• 否则，则将next标记为走到过，然后递归dfs(next, time + distance, value + values[next])（无法再次获得价值），递归结束后再将next标记为未走到过（回溯）

• 时间复杂度$O(m+n+d^k)$，其中$n=len(values)$，$m=len(edges)$，$d=4$，$k=10$。（建立邻接表耗时$O(m+n)$，递归耗时$O(d^k)$）
• 空间复杂度$O(m+n+k)$。（邻接表消耗空间$O(m+n)$，递归最大深度$O(k)$）

AC代码

C++

/*
 * @Author: LetMeFly
 * @Date: 2024-07-01 14:19:06
 * @LastEditors: LetMeFly
 * @LastEditTime: 2024-07-01 14:32:31
 */
#ifdef _WIN32
#include "_[1,2]toVector.h"
#endif

class Solution {
private:
    int ans, maxTime;
    vector<bool> visited;
    vector<int> values;
    vector<vector<pair<int, int>>> graph;  // graph[i]: [<neighbor, distance>, ...]

    void dfs(int root, int time, int value) {
        if (!root) {
            ans = max(ans, value);
        }
        for (auto [next, distance] : graph[root]) {
            if (time + distance > maxTime) {
                continue;
            }
            if (!visited[next]) {
                visited[next] = true;
                dfs(next, time + distance, value + values[next]);
                visited[next] = false;
            }
            else {
                dfs(next, time + distance, value);
            }
        }
    }
public:
    int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {
        ans = 0;
        this->maxTime = maxTime;
        visited.resize(values.size(), false);
        this->values = values;
        graph.resize(values.size());
        for (vector<int>& edge : edges) {
            graph[edge[0]].push_back({edge[1], edge[2]});
            graph[edge[1]].push_back({edge[0], edge[2]});
        }
        visited[0] = true;  // 别忘了
        dfs(0, 0, values[0]);
        return ans;
    }
};

Python

from typing import List

class Solution:
    def dfs(self, root, time, value) -> None:
        if not root:
            self.ans = max(self.ans, value)
        for next, distance in self.graph[root]:
            if time + distance > self.maxTime:
                continue
            if self.visited[next]:
                self.dfs(next, time + distance, value)
            else:
                self.visited[next] = True
                self.dfs(next, time + distance, value + self.values[next])
                self.visited[next] = False
    
    def maximalPathQuality(self, values: List[int], edges: List[List[int]], maxTime: int) -> int:
        self.ans = 0
        self.maxTime = maxTime
        self.values = values
        self.graph = [[] for _ in range(len(values))]
        for x, y, d in edges:
            self.graph[x].append((y, d))
            self.graph[y].append((x, d))
        self.visited = [False] * len(values)
        self.visited[0] = True
        self.dfs(0, 0, values[0])
        return self.ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/140101479