993.二叉树的堂兄弟节点

【LetMeFly】993.二叉树的堂兄弟节点：深度优先搜索(BFS)

力扣题目链接：https://leetcode.cn/problems/cousins-in-binary-tree/

在二叉树中，根节点位于深度 0 处，每个深度为 k 的节点的子节点位于深度 k+1 处。

如果二叉树的两个节点深度相同，但 父节点不同 ，则它们是一对堂兄弟节点。

我们给出了具有唯一值的二叉树的根节点 root ，以及树中两个不同节点的值 x 和 y 。

只有与值 x 和 y 对应的节点是堂兄弟节点时，才返回 true 。否则，返回 false。

 

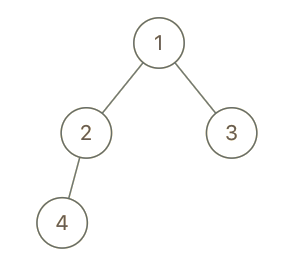
示例 1：

输入：root = [1,2,3,4], x = 4, y = 3
输出：false

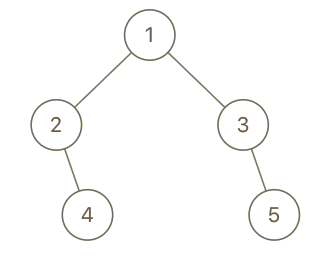
示例 2：

输入：root = [1,2,3,null,4,null,5], x = 5, y = 4
输出：true

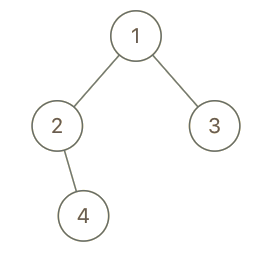
示例 3：

输入：root = [1,2,3,null,4], x = 2, y = 3
输出：false

 

提示：

• 二叉树的节点数介于 2 到 100 之间。
• 每个节点的值都是唯一的、范围为 1 到 100 的整数。

 

方法一：深度优先搜索(BFS)

两个节点是堂兄弟节点当且仅当两节点深度相同且父节点不同。

因此，我们写一个深度优先搜索函数，若搜到了x节点或y节点，则记录其父节点和深度。

最终看是否是堂兄弟节点即可。

• 时间复杂度$O(size(tree))$
• 空间复杂度$O(size(tree))$

AC代码

C++

class Solution {
private:
    int x, y;
    TreeNode* x_father, *y_father;
    int x_depth, y_depth;

    void dfs(TreeNode* root, int depth, TreeNode* father) {
        if (!root) {
            return ;
        }
        if (root->val == x) {
            x_father = father;
            x_depth = depth;
        }
        if (root->val == y) {
            y_father = father;
            y_depth = depth;
        }
        dfs(root->left, depth + 1, root);
        dfs(root->right, depth + 1, root);
    }
public:
    bool isCousins(TreeNode* root, int x, int y) {
        this->x = x, this->y = y;
        dfs(root, 0, nullptr);
        return x_father != y_father && x_depth == y_depth;
    }
};

Python

# from typing import Optional

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def dfs(self, root: Optional[TreeNode], depth: int, father: Optional[TreeNode]) -> None:
        if not root:
            return
        if root.val == self.x:
            self.x_father = father
            self.x_depth = depth
        if root.val == self.y:
            self.y_father = father
            self.y_depth = depth
        self.dfs(root.left, depth + 1, root)
        self.dfs(root.right, depth + 1, root)
    
    def isCousins(self, root: TreeNode, x: int, y: int) -> bool:
        self.x = x
        self.y = y
        self.dfs(root, 0, None)
        return self.x_father != self.y_father and self.x_depth == self.y_depth

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136078040