1599.经营摩天轮的最大利润

【LetMeFly】1599.经营摩天轮的最大利润

力扣题目链接：https://leetcode.cn/problems/maximum-profit-of-operating-a-centennial-wheel/

你正在经营一座摩天轮，该摩天轮共有 4 个座舱 ，每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱，但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。

给你一个长度为 n 的数组 customers ， customers[i] 是在第 i 次轮转（下标从 0 开始）之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ，一旦该座舱再次抵达地面，他们就会离开座舱结束游玩。

你可以随时停下摩天轮，即便是 在服务所有游客之前 。如果你决定停止运营摩天轮，为了保证所有游客安全着陆，将免费进行所有后续轮转 。注意，如果有超过 4 位游客在等摩天轮，那么只有 4 位游客可以登上摩天轮，其余的需要等待 下一次轮转 。

返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案，则返回 -1 。

 

示例 1：

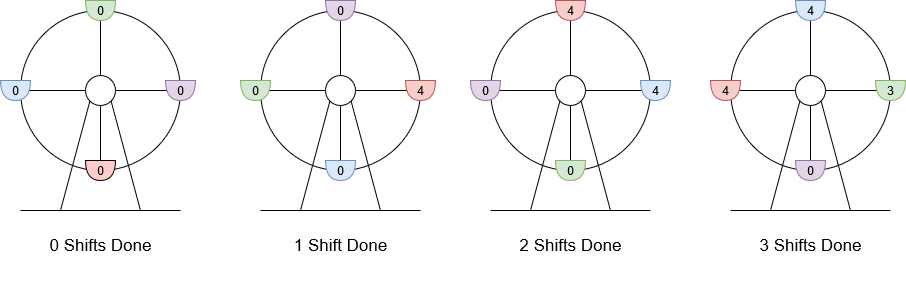
输入：customers = [8,3], boardingCost = 5, runningCost = 6
输出：3
解释：座舱上标注的数字是该座舱的当前游客数。
1. 8 位游客抵达，4 位登舱，4 位等待下一舱，摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。
2. 3 位游客抵达，4 位在等待的游客登舱，其他 3 位等待，摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。
3. 最后 3 位游客登舱，摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。
轮转 3 次得到最大利润，最大利润为 $37 。

示例 2：

输入：customers = [10,9,6], boardingCost = 6, runningCost = 4
输出：7
解释：
1. 10 位游客抵达，4 位登舱，6 位等待下一舱，摩天轮轮转。当前利润为 4 * $6 - 1 * $4 = $20 。
2. 9 位游客抵达，4 位登舱，11 位等待（2 位是先前就在等待的，9 位新加入等待的），摩天轮轮转。当前利润为 8 * $6 - 2 * $4 = $40 。
3. 最后 6 位游客抵达，4 位登舱，13 位等待，摩天轮轮转。当前利润为 12 * $6 - 3 * $4 = $60 。
4. 4 位登舱，9 位等待，摩天轮轮转。当前利润为 * $6 - 4 * $4 = $80 。
5. 4 位登舱，5 位等待，摩天轮轮转。当前利润为 20 * $6 - 5 * $4 = $100 。
6. 4 位登舱，1 位等待，摩天轮轮转。当前利润为 24 * $6 - 6 * $4 = $120 。
7. 1 位登舱，摩天轮轮转。当前利润为 25 * $6 - 7 * $4 = $122 。
轮转 7 次得到最大利润，最大利润为$122 。

示例 3：

输入：customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
输出：-1
解释：
1. 3 位游客抵达，3 位登舱，0 位等待，摩天轮轮转。当前利润为 3 * $1 - 1 * $92 = -$89 。
2. 4 位游客抵达，4 位登舱，0 位等待，摩天轮轮转。当前利润为 is 7 * $1 - 2 * $92 = -$177 。
3. 0 位游客抵达，0 位登舱，0 位等待，摩天轮轮转。当前利润为 7 * $1 - 3 * $92 = -$269 。
4. 5 位游客抵达，4 位登舱，1 位等待，摩天轮轮转。当前利润为 12 * $1 - 4 * $92 = -$356 。
5. 1 位游客抵达，2 位登舱，0 位等待，摩天轮轮转。当前利润为 13 * $1 - 5 * $92 = -$447 。
利润永不为正，所以返回 -1 。

 

提示：

• n == customers.length
• 1 <= n <= 105
• 0 <= customers[i] <= 50
• 1 <= boardingCost, runningCost <= 100

题目描述

首先需要重新描述一下题面（这道题的中文体面翻译得有些抽象）

这道题的意思是：摩天轮每运行一个舱位需要花费成本$runningCost$元，每个舱位最多乘坐$4$名乘客，每名乘客收费$boardingCost$元。

摩天轮匀速运行$i$个舱位时会有$customers[i]$个新乘客前来排队，乘客左上摩天轮后至少运行一个舱位，然后你可以随时停止摩天轮的运行（管他乘客是否还在半空中）

黑心的商人啊，唯有利益能进入他的视线！

方法一：模拟 + 贪心

使用以下几个变量：

• ans：答案answer的缩写，用于记录答案（运行多少次最佳）
• maxEarn：最多获利多少元
• nowEarn：这次运行后，获利多少元
• customerInLine：到目前为止共有多少乘客在排队
• times：运行了多少次

只需要不断模拟，直到所有乘客都上了🎡

期间记录每次启动摩天轮后的总利润（$原始利润 + 本舱乘客数 \times 每位乘客费用 - 🎡转动一个舱位的成本$）

如果本次利润大于历史最佳利润maxEarn，就更新maxEarn和ans。

为什么我要给这种解法打上一个“贪心”的Tag呢？因为黑心的商人有一个原则：不管乘客之间是否相互认识，尽量把一舱塞满，没有新乘客了不让旧乘客下来就关🎡

• 时间复杂度$O(len(customers) + \sum_{i=0}^{i<len(customer)} customers[i])$。复杂度是乘客列表的长度和乘客数量之和（除以4）
• 空间复杂度$O(1)$

AC代码

C++

class Solution {
public:
    int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {
        int ans = 0;
        int maxEarn = 0;
        int nowEarn = 0;
        int customerInLine = 0;
        int times = 0;
        while (true) {
            if (times < customers.size()) {
                customerInLine += customers[times];
            }
            times++;
            int thisCustomer = min(4, customerInLine);
            nowEarn += thisCustomer * boardingCost - runningCost;
            if (nowEarn > maxEarn) {
                maxEarn = nowEarn;
                ans = times;
            }
            customerInLine -= thisCustomer;
            if (!customerInLine && times >= customers.size()) {
                break;
            }
        }
        return ans ? ans : -1;
    }
};

Python

# from typing import List


class Solution:
    def minOperationsMaxProfit(self, customers: List[int], boardingCost: int, runningCost: int) -> int:
        ans = 0
        maxEarn = 0
        nowEarn = 0
        customerInLine = 0
        times = 0
        while True:
            if times < len(customers):
                customerInLine += customers[times]
            times += 1
            thisCustomer = min(4, customerInLine)
            customerInLine -= thisCustomer
            nowEarn += thisCustomer * boardingCost - runningCost
            if nowEarn > maxEarn:
                maxEarn = nowEarn
                ans = times
            if not customerInLine and times >= len(customers):
                break
        return ans if ans else -1

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/129345304