864.获取所有钥匙的最短路径

【LetMeFly】864.获取所有钥匙的最短路径：广搜 + 状压

力扣题目链接：https://leetcode.cn/problems/shortest-path-to-get-all-keys/

给定一个二维网格 grid ，其中：

• '.' 代表一个空房间
• '#' 代表一堵
• '@' 是起点
• 小写字母代表钥匙
• 大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 k 为 钥匙/锁 的个数，且满足 1 <= k <= 6，字母表中的前 k 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

 

示例 1：

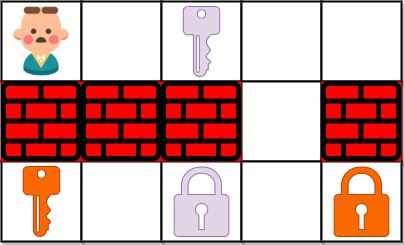
输入：grid = ["@.a.#","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

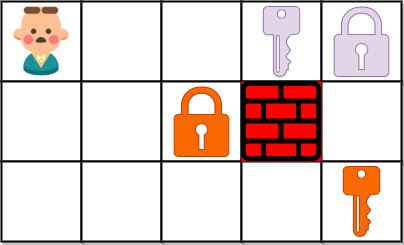
输入：grid = ["@..aA","..B#.","....b"]
输出：6

示例 3:

输入: grid = ["@Aa"]
输出: -1

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'
• 钥匙的数目范围是 [1, 6] 
• 每个钥匙都对应一个 不同 的字母
• 每个钥匙正好打开一个对应的锁

方法一：广搜 + 状压

如果不考虑钥匙和锁的问题，那么一个简单的广搜就解决了。

广搜是“走完一步能到达的位置”，然后“走完两步能到达的位置”，“……”

因此第一次搜到终点所走的步数即为答案。

本题中，增加了钥匙与锁，那么，不如把普通广搜的“位置”替换为“状态”

其中，状态包含：坐标和钥匙搜集情况

如果两次到达“同一位置”时所携带的钥匙情况不同，那么我们就认为这是“两种状态”

怎么处理钥匙收集情况呢？地图中最多有6把钥匙，因此我们可以用6位二进制数来分别代表6把钥匙。某位为1代表已获得该钥匙，0代表未获得。

这样，我们就可以把普通的广搜：

struct Node {
	int x, y;
	int step;
};

queue<Node> q;
q.push({startX, startY, 0});
bool visited[n][m] = {false};
visited[startX][startY] = true;

while (q.size()) {
    auto [thisX, thisY, thisStep] = q.front();
    q.pop();
    for (int d = 0; d < 4; d++) {
		int tx = x + directions[d][0];
		int ty = y + directions[d][1];
		if (tx >= 0 && tx < n && ty >= 0 && ty < n) {
			if (!visited[tx][ty]) {
				visited[tx][ty] = true;
				q.push({tx, ty, thisStep + 1});
				if (tx == targetX && ty == targetY) {
					return thisStep + 1;
				}
			}
		}
	}
}

return -1;

修改为：

struct Node {
	int x, y;
	int mask;  // Change
	int step;
};

queue<Node> q;
q.push({startX, startY, 0, 0});
bool visited[n][m] = {false};
visited[startX][startY][1 << keyNum] = true;

while (q.size()) {
    auto [thisX, thisY, thisMask, thisStep] = q.front();
    q.pop();
    for (int d = 0; d < 4; d++) {
		int tx = x + directions[d][0];
		int ty = y + directions[d][1];
		if (tx >= 0 && tx < n && ty >= 0 && ty < n) {
			int newMask = mask;  // Change
			if (isKey(grid[tx][ty])) {
				newMask |= (1 << getTh(grid[tx][ty]));
			}
			if (!visited[tx][ty][newMask]) {  // Change:  visited[tx][ty] -> visited[tx][ty][newMask]
				visited[tx][ty][newMask] = true;
				q.push({tx, ty, newMask, thisStep + 1});
				if (tx == targetX && ty == targetY && newMask == AllKeyMask()) {
					return thisStep + 1;
				}
			}
		}
	}
}

return -1;

说白了就是在广搜“位置”的基础上加一个“钥匙状态”

之后在广搜的过程中：

• 遇到“未到达过的空地”，就尝试到达（广搜）
• 遇到“钥匙”，就计算获得钥匙后的新状态，若“钥匙坐标&新状态”未到达过，就尝试到达（广搜）
• 遇到“锁”，就看当前的“钥匙状态”中是否包含这把锁的钥匙，若“包含钥匙&锁的位置状态未到达过”，就尝试到达（广搜）

广搜期间，一旦出现“获得一把钥匙后 集齐了所有的钥匙”，就返回当前步数作为答案。

广搜结束（未集齐全部钥匙）则返回-1

• 时间复杂度$O(nm\times k^2)$，其中$gird.size() = n\times m$，钥匙数量未$k$
• 空间复杂度$O(nm\times k^2)$

AC代码

C++

struct MyNode {
    int x, y;
    int mask;
    int step;

    MyNode(int x, int y) : x(x), y(y), mask(0), step(0) {}
};

const int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};

class Solution {
public:
    int shortestPathAllKeys(vector<string>& grid) {
        int startX, startY;
        int cntLock = 0;
        int n = grid.size(), m = grid[0].size();
        int key2th[26];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (islower(grid[i][j])) {
                    key2th[grid[i][j] - 'a'] = cntLock++;
                }
                else if (grid[i][j] == '@') {
                    startX = i, startY = j;
                }
            }
        }
        vector<vector<vector<bool>>> visited(n, vector<vector<bool>>(m, vector<bool>(1 << cntLock, false)));
        queue<MyNode> q;
        q.push(MyNode(startX, startY));
        visited[startX][startY][0] = true;
        while (q.size()) {
            MyNode thisNode = q.front();
            q.pop();
            int thisX = thisNode.x, thisY = thisNode.y, thisMask = thisNode.mask;
            // if (thisX == 1 && thisY == 4) {
            //     puts("Debug begin");  //********
            // }
            for (int d = 0; d < 4; d++) {
                int tx = thisX + directions[d][0], ty = thisY + directions[d][1];
                if (tx >= 0 && tx < n && ty >= 0 && ty < m && grid[tx][ty] != '#') {
                    if (grid[tx][ty] == '.' || grid[tx][ty] == '@') {  // @也是空地！！！
                        if (!visited[tx][ty][thisMask]) {
                            visited[tx][ty][thisMask] = true;
                            MyNode newNode = thisNode;
                            newNode.x = tx, newNode.y = ty;
                            newNode.step++;
                            q.push(newNode);
                        }
                    }
                    else if (islower(grid[tx][ty])) {
                        int toMask = thisMask | (1 << key2th[grid[tx][ty] - 'a']);
                        if (!visited[tx][ty][toMask]) {
                            visited[tx][ty][toMask] = true;
                            MyNode newNode = thisNode;
                            newNode.x = tx, newNode.y = ty;
                            newNode.step++;
                            newNode.mask = toMask;
                            q.push(newNode);
                            if (toMask == (1 << cntLock) - 1) {
                                return newNode.step; 
                            }
                        }
                    }
                    else if (isupper(grid[tx][ty])) {
                        if (thisMask & (1 << key2th[grid[tx][ty] - 'A'])) {
                            if (!visited[tx][ty][thisMask]) {
                                visited[tx][ty][thisMask] = true;
                                MyNode newNode = thisNode;
                                newNode.x = tx, newNode.y = ty;
                                newNode.step++;
                                q.push(newNode);
                            }
                        }
                    }
                }
            }
        }
        return -1;
    }
};

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/127784094