【LetMeFly】1235.规划兼职工作:[离散化:多次哈希 + DPx1] | [二分查找 + DP]
力扣题目链接:https://leetcode.cn/problems/maximum-profit-in-job-scheduling/
你打算利用空闲时间来做兼职工作赚些零花钱。
这里有 n 份兼职工作,每份工作预计从 startTime[i] 开始到 endTime[i] 结束,报酬为 profit[i]。
给你一份兼职工作表,包含开始时间 startTime,结束时间 endTime 和预计报酬 profit 三个数组,请你计算并返回可以获得的最大报酬。
注意,时间上出现重叠的 2 份工作不能同时进行。
如果你选择的工作在时间 X 结束,那么你可以立刻进行在时间 X 开始的下一份工作。
示例 1:
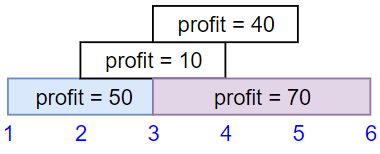
输入:startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出:120
解释:
我们选出第 1 份和第 4 份工作,
时间范围是 [1-3]+[3-6],共获得报酬 120 = 50 + 70。
示例 2:
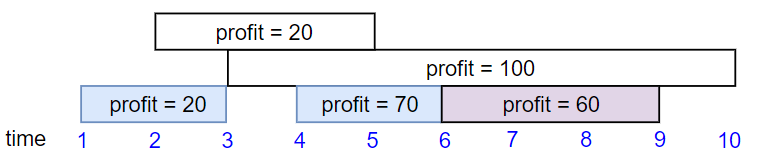
输入:startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
输出:150
解释:
我们选择第 1,4,5 份工作。
共获得报酬 150 = 20 + 70 + 60。
示例 3:

输入:startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
输出:6
提示:
1 <= startTime.length == endTime.length == profit.length <= 5 * 10^41 <= startTime[i] < endTime[i] <= 10^91 <= profit[i] <= 10^4
方法一:离散化:多次哈希 + DPx1
我们将所有出现过的时间记录下来并排序,那么我们就只需要考虑“出现过的时间”这些特殊节点,最多一共$2n$个节点。
假设一共有$n$个节点($appearedTime.size() = n$),我们建立一个长度为$n$的$dp$数组,其中$dp[i]$代表到时间$appearedTime[i]$为止的最大获利。
$dp[i] = \max{dp[i - 1], dp[第t份工作的开始时间在appearedTime中的下标] + profit[t]}$,其中$endTime[t] = appearedTime[i]$
什么意思呢?就是假如有一份工作在$appearedTime[i]$时刻结束,那么选择这份工作的话获利为$这份工作开始时的最大获利 + 这份工作的工资 = dp[这份工作开始时间对应的index] + profit[这份工作]$
以上所有需要用到的东西,均由哈希表映射即可。
如何处理出现过的时间节点
首先将所有出现过的时间放入哈希表中,然后将哈希表中的所有时间取出来,再排个序
1
2
3
4
5
6
7
8
9
10
11
12
13
| int n = startTime.size();
unordered_set<int> appearedTimeSet;
for (int i = 0; i < n; i++) {
appearedTimeSet.insert(startTime[i]);
appearedTimeSet.insert(endTime[i]);
}
vector<int> appearedTime;
for (const int& t : appearedTimeSet) {
appearedTime.push_back(t);
}
sort(appearedTime.begin(), appearedTime.end());
|
如何由结束时间映射到这是第几份工作
将<工作结束时间, 这是第几份工作>插入哈希表,就可以通过工作结束时间获取所有的在这个时间结束的工作
1
2
3
4
5
6
| int n = startTime.size();
unordered_multimap<int, int> endBy;
for (int i = 0; i < n; i++) {
endBy.insert({endTime[i], i});
}
|
如何由工作的开始时间映射到其在appearedTime中的index
遍历appearedTime中的时间,将<时间, 这个时间的index>插入哈希表
1
2
3
4
5
| int nTime = appearedTime.size();
unordered_map<int, int> time2loc;
for (int i = 0; i < nTime; i++) {
time2loc[appearedTime[i]] = i;
}
|
动态规划部分怎么实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| vector<int> dp(nTime);
for (int i = 1; i < nTime; i++) {
dp[i] = dp[i - 1];
auto range = endBy.equal_range(appearedTime[i]);
for_each(range.first, range.second, [&](unordered_multimap<int, int>::value_type& x) {
dp[i] = max(dp[i], dp[time2loc[startTime[x.second]]] + profit[x.second]);
});
}
return dp.back();
|
- 时间复杂度$O(\n log n)$,其中$n$是工作数量,时间复杂度主要来自排序
- 空间复杂度$O(n)$,使用了数次哈希表,每次的空间复杂度都是$O(n)$
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public:
int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
unordered_set<int> appearedTimeSet;
unordered_multimap<int, int> endBy;
int n = startTime.size();
for (int i = 0; i < n; i++) {
appearedTimeSet.insert(startTime[i]);
appearedTimeSet.insert(endTime[i]);
endBy.insert({endTime[i], i});
}
vector<int> appearedTime;
for (const int& t : appearedTimeSet) {
appearedTime.push_back(t);
}
sort(appearedTime.begin(), appearedTime.end());
int nTime = appearedTime.size();
unordered_map<int, int> time2loc;
for (int i = 0; i < nTime; i++) {
time2loc[appearedTime[i]] = i;
}
vector<int> dp(nTime);
for (int i = 1; i < nTime; i++) {
dp[i] = dp[i - 1];
auto range = endBy.equal_range(appearedTime[i]);
for_each(range.first, range.second, [&](unordered_multimap<int, int>::value_type& x) {
dp[i] = max(dp[i], dp[time2loc[startTime[x.second]]] + profit[x.second]);
});
printf("i = %d, appearedTime[%d] = %d, dp[%d] = %d\n", i, i, appearedTime[i], i, dp[i]);
}
return dp.back();
}
};
|
方法二:二分查找 + DP
方法一中我们使用了数个哈希表将时间和工作映射了起来
方法二学习自力扣官解:https://leetcode.cn/problems/maximum-profit-in-job-scheduling/solution/gui-hua-jian-zhi-gong-zuo-by-leetcode-so-gu0e/
这种方法中,$dp[i]$代表前$i$份兼职工作可以获得的最大报酬。
因此,$dp[i] = \max{dp[i-1], dp[k] + profit[i - 1]}$,其中$k$表示结束时间不超过第$i-1$份工作的开始时间的工作数量
这个$k$怎么来呢?当然是二分查找
因此我们还需要对工作按照“结束时间”从小到大排个序。
- 时间复杂度$O(\n log n)$,其中$n$是工作数量,时间复杂度主要来自排序
- 空间复杂度$O(n)$
AC代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
int n = startTime.size();
vector<vector<int>> jobs(n);
for (int i = 0; i < n; i++) {
jobs[i] = {startTime[i], endTime[i], profit[i]};
}
sort(jobs.begin(), jobs.end(), [&](const vector<int>& a, const vector<int>& b){
return a[1] < b[1];
});
vector<int> dp(n + 1);
for (int i = 1; i <= n; i++) {
int k = upper_bound(jobs.begin(), jobs.begin() + i - 1, jobs[i - 1][0], [&](int st, vector<int>& job) {
return st < job[1];
}) - jobs.begin();
dp[i] = max(dp[i - 1], dp[k] + jobs[i - 1][2]);
}
return dp[n];
}
};
|
同步发文于CSDN,原创不易,转载请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/127458533


