156.上下翻转二叉树

【LetMeFly】156.上下翻转二叉树 - 一个小巧的办法

给你一个二叉树的根节点 root ，请你将此二叉树上下翻转，并返回新的根节点。

你可以按下面的步骤翻转一棵二叉树：

1. 原来的左子节点变成新的根节点
2. 原来的根节点变成新的右子节点
3. 原来的右子节点变成新的左子节点

上面的步骤逐层进行。题目数据保证每个右节点都有一个同级节点（即共享同一父节点的左节点）且不存在子节点。

示例 1:

输入：root = [1,2,3,4,5]
输出：[4,5,2,null,null,3,1]

示例 2:

输入：root = []
输出：[]

示例 3:

输入：root = [1]
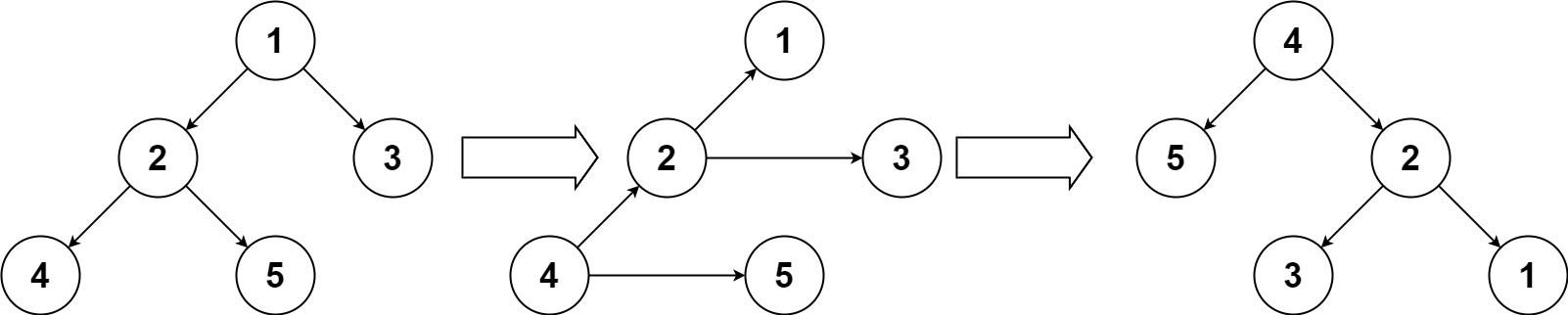
输出：[1]

提示:

• 树中节点数目在范围 $[0, 10]$ 内
• $1 \leq Node.val \leq 10$
• 树中的每个右节点都有一个同级节点（即共享同一父节点的左节点）
• 树中的每个右节点都没有子节点

思路

如果真地按照题目的描述从上到下进行反转，那么上方节点的左右子的变化会导致其原始下方节点信息的丢失。

以例1为例，如果先反转节点1、3、2，那么节点2的左右子节点4、5的信息将会丢失。

那么如果我们先反转最左子节点呢？我们很容易就能找到这棵树的最左子节点。但是，子节点不包含父节点的信息，因此仅仅通过子节点就找不到它的兄弟节点。

以例1为例，我们能很容易找到这棵树的最左节点4（也就是反转后的根节点）。但是仅凭节点4我们找不到4的父节点2，也就无法找到4的兄弟节点5。

对于这种情况，递归就是一个非常不错的选择了。

方法一：递归

综合上述两种“思路”，思路1(从上到下反转)的最大问题就是反转会导致子节点信息的丢失，思路2(从下到上反转)的最大问题就是由子节点找不到父节点。

因此我们可以定义一个反转函数reverse，假设父节点是X，左子和右子节点分别是Y和Z，那么递归函数的形式就是：

void reverse(TreeNode* X, TreeNode* Y, TreeNode* Z) {
    reverse(左子，左子->left，左子->right);  // 先反转下一层的
    
    // 再反转这一层的
    Y->left = Z, Y->right = X;
    X->left = X->right = nullptr;
    if (Z)
        Z->left = Z->right = nullptr;
}

既然思路2中子节点缺乏的是父节点，那么我们就把父、左子、右子的信息都作为参数传递给这个函数，这样就能很轻松地知道左子节点的兄弟节点。

同时，先反转下一层再反转这一层，也解决了思路1的痛点。

但是，我们还需要知道最终反转完成后的根节点啊。一种简单的方法就是反转之前，先无脑遍历一遍，找到最左子节点，就是反转后的根节点。

但是这样代码不优美(手动滑稽)，我们可以简单修改一下递归函数，就能在递归的同时返回新的根节点。

TreeNode* reverse(TreeNode* X, TreeNode* Y, TreeNode* Z) {
    TreeNode* newRoot = reverse(左子，左子->left，左子->right);  // 先反转下一层的
    
    // 再反转这一层的
    Y->left = Z, Y->right = X;
    X->left = X->right = nullptr;
    if (Z)
        Z->left = Z->right = nullptr;
    
    // 返回新节点
    return newRoot;
}

• 时间复杂度$O(n)$，其中$n$是节点个数
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
private:
    TreeNode* reverse(TreeNode* X, TreeNode* Y, TreeNode* Z) {
        if (!Y)
            return X;
        TreeNode* ans = reverse(Y, Y->left, Y->right);
        Y->left = Z, Y->right = X;
        X->left = X->right = nullptr;
        if (Z)  // Z为空节点的话就没有左右节点了
            Z->left = Z->right = nullptr;
        return ans;
    }
public:
    TreeNode* upsideDownBinaryTree(TreeNode* root) {
        if (!root)
            return root;
        return reverse(root, root->left, root->right);
    }
};

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125028889