2054.两个最好的不重叠活动：二分查找

【LetMeFly】2054.两个最好的不重叠活动：二分查找

力扣题目链接：https://leetcode.cn/problems/two-best-non-overlapping-events/

给你一个下标从 0 开始的二维整数数组 events ，其中 events[i] = [startTimei, endTimei, valuei] 。第 i 个活动开始于 startTimei ，结束于 endTimei ，如果你参加这个活动，那么你可以得到价值 valuei 。你 最多 可以参加 两个时间不重叠 活动，使得它们的价值之和 最大 。

请你返回价值之和的 最大值 。

注意，活动的开始时间和结束时间是 包括 在活动时间内的，也就是说，你不能参加两个活动且它们之一的开始时间等于另一个活动的结束时间。更具体的，如果你参加一个活动，且结束时间为 t ，那么下一个活动必须在 t + 1 或之后的时间开始。

 

示例 1:

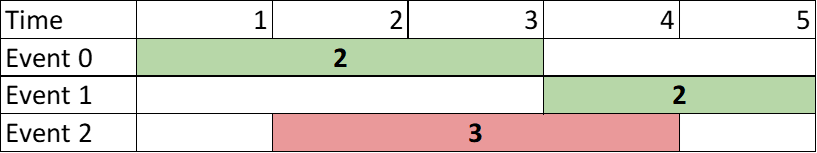
输入：events = [[1,3,2],[4,5,2],[2,4,3]]
输出：4
解释：选择绿色的活动 0 和 1 ，价值之和为 2 + 2 = 4 。

示例 2：

输入：events = [[1,3,2],[4,5,2],[1,5,5]]
输出：5
解释：选择活动 2 ，价值和为 5 。

示例 3：

输入：events = [[1,5,3],[1,5,1],[6,6,5]]
输出：8
解释：选择活动 0 和 2 ，价值之和为 3 + 5 = 8 。

 

提示：

• 2 <= events.length <= 105
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 109
• 1 <= valuei <= 106

解题方法：二分查找

如果只能选一个event，那么好说，哪个价值大选哪个；如果一定要选两个event，假设第二个event选事件e，那么第一个event一定要选结束时间早于e开始时间的所有事件中价值最大的那个。

很显然，为了枚举第一个event的可选范围，可以以结束时间为依据对所有event按从小到大排个序。

接着使用一个（有序）数组maxValue，数组中存放的内容是：到xx时刻为止，单个event的最大价值是多少。排序依据是结束时间。

遍历所有事件，对于某事件e，二分查找maxValue中小于e开始时间中最大的那个，其值加上e的价值即为第二个event选e情况下的最优解。之后更新e结束时间的单个事件最大值。

• 时间复杂度$O(n\log n)$，其中$n=len(events)$
• 空间复杂度$O(n)$

AC代码

C++

/*
 * @LastEditTime: 2025-12-23 18:58:01
 */
class Solution {
public:
    int maxTwoEvents(vector<vector<int>>& events) {
        sort(events.begin(), events.end(), [](const vector<int>& a, const vector<int>& b) {
            return a[1] < b[1];
        });
        vector<pair<int, int>> maxValue;
        int singleMax = 0, pairMax = 0;
        for (vector<int>& e : events) {
            vector<pair<int, int>>::iterator it = lower_bound(maxValue.begin(), maxValue.end(), e[0], [](const pair<int, int>& p, int value) {
                return p.first < value;
            });
            if (it != maxValue.begin()) {
                pairMax = max(pairMax, (--it)->second + e[2]);
            }
            singleMax = max(singleMax, e[2]);
            maxValue.push_back({e[1], singleMax});
        }
        return max(pairMax, singleMax);
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源