790.多米诺和托米诺平铺：难想条件的简单动态规划

【LetMeFly】790.多米诺和托米诺平铺：难想条件的简单动态规划

力扣题目链接：https://leetcode.cn/problems/domino-and-tromino-tiling/

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

 

示例 1:

输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

 

提示：

• 1 <= n <= 1000

解题方法：动态规划

力扣的@灵茶山艾府有张不错的图(来自这个题解)：

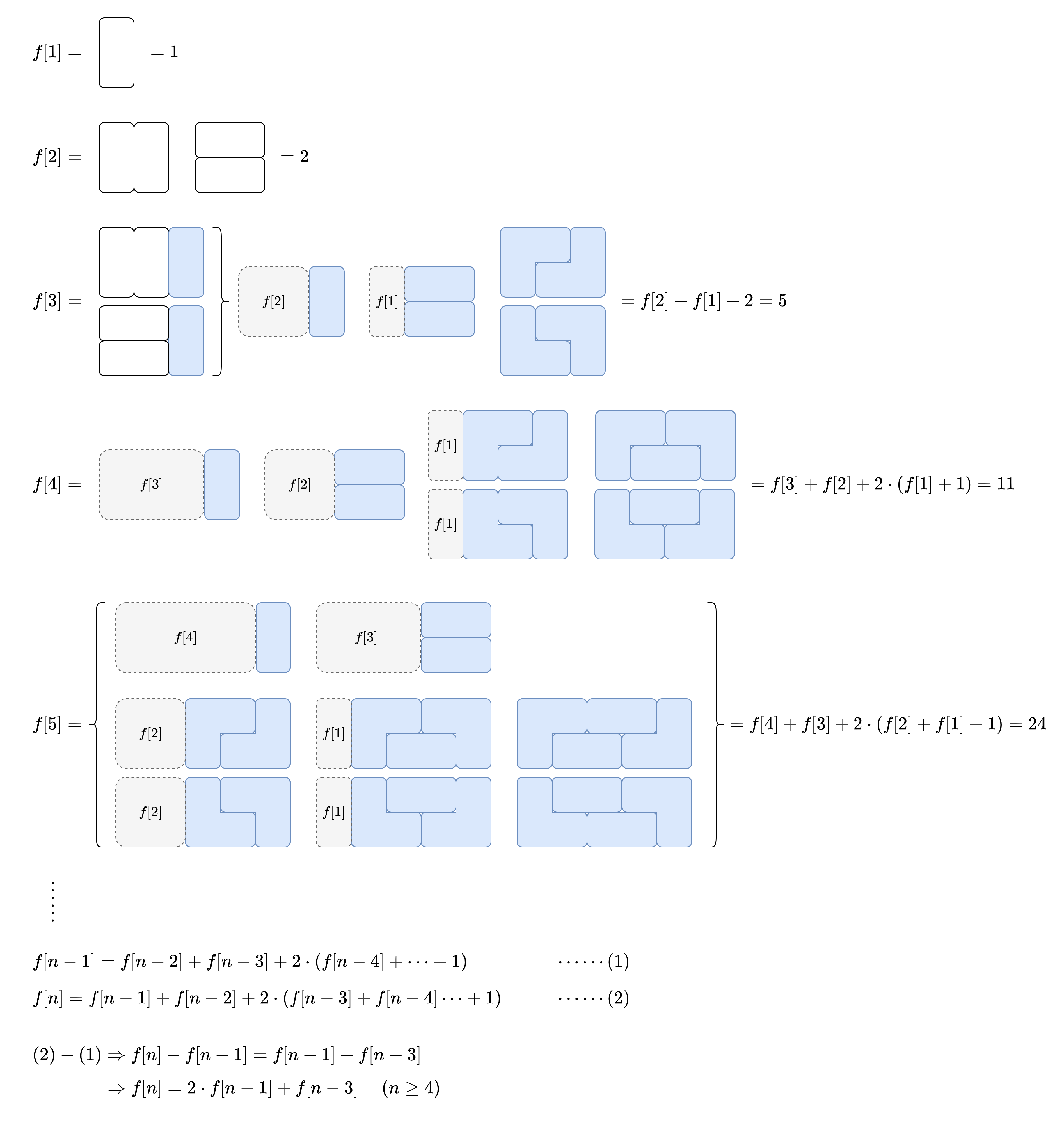
可以使用$f[i]$代表铺满$i$列的方案数，那么对于最右边的可以独立切割出来的矩形（也就是图上蓝色部分）有三种情况。

什么叫“最右边的可以独立切割出来的矩”？就是说“最右边蓝色部分无法被竖着一刀分成左右两个部分”。

因为若能竖着一刀将右边蓝色部分分成左右两个部分，那么左边部分的方案数一定已经被$f[j]$计算过了。

三种情况如下：

1. 最右边的蓝色独立矩形是一个竖着的$1\times 2$，可以在$f[i-1]$的基础上得到
2. 最右边的蓝色独立矩形是两个横着的$2\times 1$，可以在$f[i-2]$的基础上得到
3. 最右边的蓝色独立矩形完全交错排列，无法被竖着一刀分割，可以分别在$f[i-3]$、$f[i-4]$、$\cdots$、$f[0]$的基础上得到，并且每种都有上下两种摆放方式。

也就是说：$f[i]=f[i-1]+f[i-2]+2\times\sum_{j=0}^{i-3}f[j]$

但是这样的时间复杂度是$O(n^2)$，有没有一种更快的求法？有：

$f[i]-f[i-1]$是多少呢？

$$f[i]-f[i-1]=f[i-1]+f[i-2]+2\times\sum_{j=0}^{i-3}f[j]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -f[i-2]+f[i-3]+2\times\sum_{j=0}^{i-4}f[j]\ \ =f[i-1]+f[i-3]$$

所以有$f[i]=2\times f[i-1]+f[i-3]$。

实现容易推导难。

• 时间复杂度$O(n)$
• 空间复杂度$O(n)$

不难发现，求$f[i]$时只会用到$f[i-1]$和$f[i-3]$两个变量，因此实际上我们使用$4$个变量滚动式地循环使用即可将空间复杂度降低到$O(1)$。

AC代码

C++

/*
 * @Author: LetMeFly
 * @Date: 2025-05-05 21:58:06
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-05-05 22:23:11
 */
const int MOD = 1e9 + 7;

class Solution {
public:
    int numTilings(int n) {
        if (n == 1) {
            return 1;
        }
        vector<int> dp(n + 1);
        dp[0] = dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = ((dp[i - 1] * 2) % MOD + dp[i - 3]) % MOD;
        }
        return dp.back();
    }
};

Python

'''
Author: LetMeFly
Date: 2025-05-05 21:58:06
LastEditors: LetMeFly.xyz
LastEditTime: 2025-05-05 22:25:56
'''
MOD = 1000000007

class Solution:
    def numTilings(self, n: int) -> int:
        if n == 1:
            return 1
        dp = [0] * (n + 1)
        dp[0] = dp[1] = 1
        dp[2] = 2
        for i in range(3, n + 1):
            dp[i] = (dp[i - 1] * 2 + dp[i - 3]) % MOD
        return dp[-1]

Java

/*
 * @Author: LetMeFly
 * @Date: 2025-05-05 21:58:06
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-05-05 22:28:23
 */
class Solution {
    private static int MOD = 1000000007;

    public int numTilings(int n) {
        if (n == 1) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[0] = dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = ((dp[i - 1] * 2) % MOD + dp[i - 3]) % MOD;
        }
        return dp[n];
    }
}

Go

/*
 * @Author: LetMeFly
 * @Date: 2025-05-05 21:58:06
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-05-05 22:38:29
 */
package main

var MOD int = 1000000007

func numTilings(n int) int {
    if n == 1 {
        return 1
    }
    dp := make([]int, n + 1)
    dp[0] = 1
    dp[1] = 1
    dp[2] = 2
    for i := 3; i <= n; i++ {
        dp[i] = (dp[i - 1] * 2 % MOD + dp[i - 3]) % MOD
    }
    return dp[n]
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源