935.骑士拨号器

【LetMeFly】935.骑士拨号器：动态规划(DP)

力扣题目链接：https://leetcode.cn/problems/knight-dialer/

象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 L 的形状)。

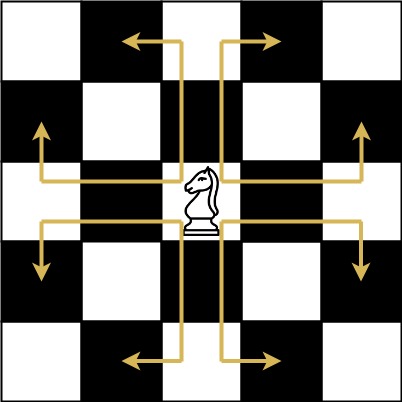
象棋骑士可能的移动方式如下图所示:

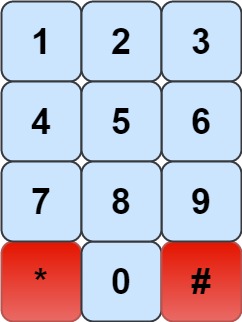
我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，所以输出答案模 109 + 7.

 

示例 1：

输入：n = 1
输出：10
解释：我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2：

输入：n = 2
输出：20
解释：我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3：

输入：n = 3131
输出：136006598
解释：注意取模

 

提示：

• 1 <= n <= 5000

解题方法：动态规划

使用$dp[i]$代表当前这一步号码为$i$时的总方案数，初始值$dp[0] = dp[1] = \cdots = dp[9] = 0$。

预先打表一个$canFrom$数组，$canFrom[i]$代表能从哪些号码一步到达号码$i$:

canFrom = {
    {4, 6},  // 0可以来自4，6
    {6, 8},
    {7, 9},
    {4, 8},
    {3, 9, 0},
    {},
    {1, 7, 0},
    {2, 6},
    {1, 3},
    {2, 4}
};

之后从第2个号码开始，假设当前号码为$i$，则有状态转移方程：

$$dp[i] = sum(dp[from]), from \in canFrom[i]$$

• 时间复杂度$O(n)$，其中常数比较大，为canFrom数组中的数据量20
• 空间复杂度$O(1)$

AC代码

C++

const vector<vector<int>> canFrom = {
    {4, 6},  // 0可以来自4，6
    {6, 8},
    {7, 9},
    {4, 8},
    {3, 9, 0},
    {},
    {1, 7, 0},
    {2, 6},
    {1, 3},
    {2, 4}
};
const int mod = 1e9 + 7;

class Solution {
public:
    int knightDialer(int n) {
        int last[10], now[10];
        fill(last, last + 10, 1);
        for (int i = 2; i <= n; i++) {
            memset(now, 0, sizeof(now));
            for (int j = 0; j < 10; j++) {
                for (int from : canFrom[j]) {
                    now[j] = (now[j] + last[from]) % mod;
                }
            }
            memcpy(last, now, sizeof(now));
        }
        // return accumulate(last, last + 10, 0);  // WA，这里没取模
        int ans = 0;
        for (int i = 0; i < 10; i++) {
            ans = (ans + last[i]) % mod;
        }
        return ans;
    }
};

Python

# AC,57.50%,56.76%
CAN_FROM = [
    [4, 6],
    [6, 8],
    [7, 9],
    [4, 8],
    [3, 9, 0],
    [], 
    [1, 7, 0],
    [2, 6],
    [1, 3],
    [2, 4]
]
MOD = 1_000_000_007

class Solution:
    def knightDialer(self, n: int) -> int:
        last = [1] * 10
        for _ in range(n - 1):
            now = [0] * 10
            for i in range(10):
                for j in CAN_FROM[i]:
                    now[i] = (now[i] + last[j]) % MOD
            last = now
        return sum(last) % MOD

Java

import java.util.Arrays;

class Solution {
    private final int[][] canFrom = {
        {4, 6},  // 0可以来自4，6
        {6, 8},
        {7, 9},
        {4, 8},
        {3, 9, 0},
        {},
        {1, 7, 0},
        {2, 6},
        {1, 3},
        {2, 4}
    };
    private final int mod = 1000000007;

    public int knightDialer(int n) {
        int[] last = new int[10];
        int[] now = new int[10];
        Arrays.fill(last, 1);
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < 10; j++) {
                for (int from : canFrom[j]) {
                    now[j] = (now[j] + last[from]) % mod;
                }
            }
            last = now;
        }
        int ans = 0;
        for (int i = 0; i < 10; i++) {
            ans = (ans + last[i]) % mod;
        }
        return ans;
    }
}

Go

package main

var canFrom = [][]int{
    {4, 6},  // 0可以来自4，6
    {6, 8},
    {7, 9},
    {4, 8},
    {3, 9, 0},
    {},
    {1, 7, 0},
    {2, 6},
    {1, 3},
    {2, 4},
};
var mod = 1000000007

func knightDialer(n int) (ans int) {
    last := make([]int, 10)
    for i := range last {
        last[i] = 1
    }
    for i := 2; i <= n; i++ {
        now := make([]int, 10)
        for j := 0; j < 10; j++ {
            for _, from := range canFrom[j] {
                now[j] = (now[j] + last[from]) % mod
            }
        }
        last = now
    }
    for i := range last {
        ans = (ans + last[i]) % mod;
    }
    return
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/144375933