3240.最少翻转次数使二进制矩阵回文 II

【LetMeFly】3240.最少翻转次数使二进制矩阵回文 II：分类讨论

力扣题目链接：https://leetcode.cn/problems/minimum-number-of-flips-to-make-binary-grid-palindromic-ii/

给你一个 m x n 的二进制矩阵 grid 。

如果矩阵中一行或者一列从前往后与从后往前读是一样的，那么我们称这一行或者这一列是 回文 的。

你可以将 grid 中任意格子的值 翻转 ，也就是将格子里的值从 0 变成 1 ，或者从 1 变成 0 。

请你返回 最少 翻转次数，使得矩阵中 所有 行和列都是 回文的 ，且矩阵中 1 的数目可以被 4 整除 。

 

示例 1：

输入：grid = [[1,0,0],[0,1,0],[0,0,1]]

输出：3

解释：

示例 2：

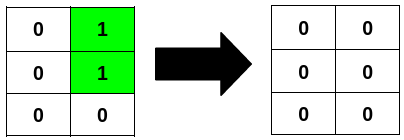
输入：grid = [[0,1],[0,1],[0,0]]

输出：2

解释：

示例 3：

输入：grid = [[1],[1]]

输出：2

解释：

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m * n <= 2 * 105
  • 0 <= grid[i][j] <= 1

解题方法：分类讨论

step1: 先不考虑4的倍数个1，计算最小翻转次数

step2: 再考虑1的个数问题：

  • 偶数行偶数列：(1必定是4的倍数个)直接返回

  • 奇数行偶数列：看中间那一行有多少对11和多少对10/01

    • 偶数对11：(step1时可以把所有01/10变成00)直接返回

    • 奇数对11：看有无10/01：

      • 有10/01：(step1时把中间这一行的其中一对10/01变成11)直接返回
      • 无10/01：(step2必须把一对11变成00)step1结果+2后返回

  • 偶数行奇数列：和奇数行偶数列同理

  • 奇数行奇数列：要看“最中心元素”和“中间行中间列除最中间元素外的部分”两部分

    • 最中心元素：

      • 若为1：(必须变为0)step1+1
      • 若为0：step1不变

    • 中间行中间列除最中间元素外的部分：类似奇数行偶数列，统计这些元素中所有的11对和10/01对，之后同理

  • 时间复杂度$O(nm)$

  • 空间复杂度$O(1)$

不难发现，也可以直接判定是否存在“中间行”和“中间列”进行代码简化。

AC代码

C++ 复杂版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
/*
step1: 先不考虑4的倍数个1，计算最小翻转次数

step2: 再考虑1的个数问题：

偶数行偶数列：(1必定是4的倍数个)直接返回
奇数行偶数列：看中间那一行有多少对11和多少对10/01
    + 偶数对11：(step1时可以把所有01/10变成00)直接返回
    + 奇数对11：看有无10/01：
        + 有10/01：(step1时把中间这一行的其中一对10/01变成11)直接返回
        + 无10/01：(step2必须把一对11变成00)step1结果+2后返回
偶数行奇数列：和奇数行偶数列同理
奇数行奇数列：要看“最中心元素”和“中间行中间列除最中间元素外的部分”两部分
    + 最中心元素：
        + 若为1：(必须变为0)step1+1
        + 若为0：step1不变
    + 中间行中间列除最中间元素外的部分：类似奇数行偶数列，统计这些元素中所有的11对和10/01对，之后同理
*/
class Solution {
public:
    int minFlips(vector<vector<int>>& grid) {
        int ans = 0;
        int n = grid.size(), m = grid[0].size();
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < m / 2; j++) {
                int cnt1 = grid[i][j] + grid[i][m - j - 1] + grid[n - i - 1][j] + grid[n - i - 1][m - j - 1];
                ans += min(cnt1, 4 - cnt1);
            }
        }
        if (n % 2 == 0 && m % 2 == 0) {
            return ans;
        } else if (n % 2 == 1 && m % 2 == 0) {
            int cnt11 = 0, cnt0110 = 0;
            for (int j = 0; j < m / 2; j++) {
                if (grid[n / 2][j] == grid[n / 2][m - j - 1]) {
                    if (grid[n / 2][j] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
            ans += cnt0110;
            if (cnt11 % 2 == 0 || cnt0110 > 0) {
                return ans;
            } else {
                return ans + 2;
            }
        } else if (n % 2 == 0 && m % 2 == 1) {
            int cnt11 = 0, cnt0110 = 0;
            for (int i = 0; i < n / 2; i++) {
                if (grid[i][m / 2] == grid[n - i - 1][m / 2]) {
                    if (grid[i][m / 2] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
            ans += cnt0110;
            if (cnt11 % 2 == 0 || cnt0110 > 0) {
                return ans;
            } else {
                return ans + 2;
            }
        } else {
            if (grid[n / 2][m / 2]) {
                ans++;
            }
            int cnt11 = 0, cnt0110 = 0;
            for (int j = 0; j < m / 2; j++) {
                if (grid[n / 2][j] == grid[n / 2][m - j - 1]) {
                    if (grid[n / 2][j] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
            for (int i = 0; i < n / 2; i++) {
                if (grid[i][m / 2] == grid[n - i - 1][m / 2]) {
                    if (grid[i][m / 2] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
            ans += cnt0110;
            if (cnt11 % 2 == 0 || cnt0110 > 0) {
                return ans;
            } else {
                return ans + 2;
            }
        }
    }
};

C++ 简化版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int minFlips(vector<vector<int>>& grid) {
        int ans = 0;
        int n = grid.size(), m = grid[0].size();
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < m / 2; j++) {
                int cnt1 = grid[i][j] + grid[i][m - j - 1] + grid[n - i - 1][j] + grid[n - i - 1][m - j - 1];
                ans += min(cnt1, 4 - cnt1);
            }
        }
        if (n % 2 && m % 2) {
            ans += grid[n / 2][m / 2];
        }
        int cnt11 = 0, cnt0110 = 0;
        if (n % 2 == 1) {
            for (int j = 0; j < m / 2; j++) {
                if (grid[n / 2][j] == grid[n / 2][m - j - 1]) {
                    if (grid[n / 2][j] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
        }
        if (m % 2 == 1) {
            for (int i = 0; i < n / 2; i++) {
                if (grid[i][m / 2] == grid[n - i - 1][m / 2]) {
                    if (grid[i][m / 2] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
            
        }
        ans += cnt0110;
        if (cnt11 % 2 == 0 || cnt0110 > 0) {
            return ans;
        } else {
            return ans + 2;
        }
        return ans;
    }
};

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from typing import List

class Solution:
    def minFlips(self, grid: List[List[int]]) -> int:
        ans = 0
        n, m = len(grid), len(grid[0])
        for i in range(n // 2):
            for j in range(m // 2):
                cnt1 = grid[i][j] + grid[i][m - j - 1] + grid[n - i - 1][j] + grid[n - i - 1][m - j - 1]
                ans += min(cnt1, 4 - cnt1)
        if n % 2 and m % 2:
            ans += grid[n // 2][m // 2]
        cnt11, cnt1001 = 0, 0
        if n % 2:
            for j in range(m // 2):
                if grid[n // 2][j] == grid[n // 2][m - j - 1]:
                    if grid[n // 2][j] == 1:
                        cnt11 += 1
                else:
                    cnt1001 += 1
        if m % 2:
            for i in range(n // 2):
                if grid[i][m // 2] == grid[n - i - 1][m // 2]:
                    if grid[i][m // 2] == 1:
                        cnt11 += 1
                else:
                    cnt1001 += 1
        ans += cnt1001
        if cnt11 % 2 and not cnt1001:
            ans += 2
        return ans

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int minFlips(int[][] grid) {
        int ans = 0;
        int n = grid.length, m = grid[0].length;
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < m / 2; j++) {
                int cnt1 = grid[i][j] + grid[i][m - j - 1] + grid[n - i - 1][j] + grid[n - i - 1][m - j - 1];
                ans += Math.min(cnt1, 4 - cnt1);
            }
        }
        if (n % 2 == 1 && m % 2 == 1) {
            ans += grid[n / 2][m / 2];
        }
        int cnt11 = 0, cnt0110 = 0;
        if (n % 2 == 1) {
            for (int j = 0; j < m / 2; j++) {
                if (grid[n / 2][j] == grid[n / 2][m - j - 1]) {
                    if (grid[n / 2][j] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
        }
        if (m % 2 == 1) {
            for (int i = 0; i < n / 2; i++) {
                if (grid[i][m / 2] == grid[n - i - 1][m / 2]) {
                    if (grid[i][m / 2] == 1) {
                        cnt11++;
                    }
                } else {
                    cnt0110++;
                }
            }
        }
        ans += cnt0110;
        if (cnt11 % 2 == 1 && cnt0110 == 0) {
            ans += 2;
        }
        return ans;
    }
}

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
package main

func minFlips(grid [][]int) (ans int) {
    n, m := len(grid), len(grid[0])
    for i := 0; i < n / 2; i++ {
        for j := 0; j < m / 2; j++ {
            cnt1 := grid[i][j] + grid[i][m - j - 1] + grid[n - i - 1][j] + grid[n - i - 1][m - j - 1]
            ans += min(cnt1, 4 - cnt1)
        }
    }
    if n % 2 == 1 && m % 2 == 1 {
        ans += grid[n / 2][m / 2]
    }
    cnt11, cnt1001 := 0, 0
    if n % 2 == 1 {
        for j := 0; j < m / 2; j++ {
            if grid[n / 2][j] == grid[n / 2][m - j - 1] {
                if grid[n / 2][j] == 1 {
                    cnt11++
                }
            } else {
                cnt1001++
            }
        }
    }
    if m % 2 == 1 {
        for i := 0; i < n / 2; i++ {
            if grid[i][m / 2] == grid[n - i - 1][m / 2] {
                if (grid[i][m / 2] == 1) {
                    cnt11++
                }
            } else {
                cnt1001++
            }
        }
    }
    ans += cnt1001
    if cnt11 % 2 == 1 && cnt1001 == 0 {
        ans +=2
    }
    return
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/143816332

#题解 #中等 #双指针 #数组 #LeetCode #回文 #矩阵
3240.最少翻转次数使二进制矩阵回文 II
https://blog.letmefly.xyz/2024/11/16/LeetCode 3240.最少翻转次数使二进制矩阵回文II/
作者
Tisfy
发布于
2024年11月16日
许可协议