684.冗余连接

【LetMeFly】684.冗余连接：拓扑排序+哈希表（O(n)） 或 并查集（O(nlog n)-O(nα(n))）

力扣题目链接：https://leetcode.cn/problems/redundant-connection/

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

 

示例 1：

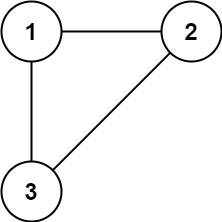
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

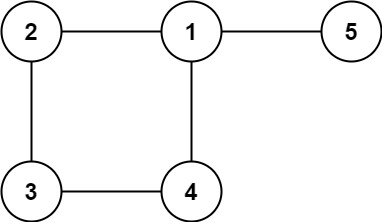
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

 

提示:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges 中无重复元素
• 给定的图是连通的 

方法一：拓扑排序（哈希表）

记录每个点的度，使用拓扑排序的思想，每次将度为1的节点所连的边移除。

最后剩下的点就是“环”中的点，将这些点放入哈希表中。

倒叙遍历“边”，第一条两个节点都出现在哈希表中的边即为所求。

• 时间复杂度$O(n)$
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> degree(edges.size() + 1);
        vector<vector<int>> graph(edges.size() + 1);
        for (vector<int>& edge : edges) {
            degree[edge[0]]++;
            degree[edge[1]]++;
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        queue<int> q;
        for (int i = 1; i <= edges.size(); i++) {
            if (degree[i] == 1) {
                q.push(i);
            }
        }
        while (q.size()) {
            int thisNode = q.front();
            q.pop();
            for (int nextNode : graph[thisNode]) {
                degree[nextNode]--;
                if (degree[nextNode] == 1) {
                    q.push(nextNode);
                }
            }
        }
        unordered_set<int> reservedNodes;
        for (int i = 1; i <= edges.size(); i++) {
            if (degree[i] > 1) {
                reservedNodes.insert(i);
            }
        }
        // for (vector<vector<int>>::iterator it = edges.rbegin(); it != edges.rend(); it++)
        for (int i = edges.size() - 1; i >= 0; i--) {
            if (reservedNodes.count(edges[i][0]) && reservedNodes.count(edges[i][1])) {
                return edges[i];
            }
        }
        return {};  // FAKE RETURN
    }
};

方法二：并查集

使用并查集将每条边的两个顶点加入同一个集合中，第一条两个顶点已经在一个集合中的边即为所求（加上这条边后就形成了环）。

• 时间复杂度最坏$O(n\log n)$，平均为$O(n\alpha(n))$（接近$O(n)$）
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
private:
    vector<int> fa;

    int find(int x) {
        if (fa[x] != x) {
            fa[x] = find(fa[x]);
        }
        return fa[x];
    }

    void union_(int x, int y) {
        fa[find(x)] = find(y);
    }
public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        fa.resize(edges.size() + 1);
        for (int i = 1; i <= edges.size(); i++) {
            fa[i] = i;
        }
        // for (vector<int>& edge : edges) {
        //     union_(edge[0], edge[1]);
        // }
        // for (int i = edges.size() - 1; i > 0; i--) {
        //     if (find(edges[i][0]) == find(edges[i][1])) {
        //         return edges[i];
        //     }
        // }
        for (vector<int>& edge : edges) {
            if (find(edge[0]) == find(edge[1])) {
                return edge;
            } else {
                union_(edge[0], edge[1]);
            }
        }
        return {};  // FAKE RETURN
    }
};

Python

from typing import List

class Solution:
    def union(self, x: int, y: int) -> None:
        self.fa[self.find(x)] = self.find(y)
    
    def find(self, x: int) -> int:
        if self.fa[x] != x:
            self.fa[x] = self.find(self.fa[x])
        return self.fa[x]

    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        self.fa = [i for i in range(len(edges) + 1)]
        for x, y in edges:
            if self.find(x) == self.find(y):
                return [x, y]
            else:
                self.union(x, y)
        return []  # FAKE RETURN

Java

class Solution {
    private int[] fa;

    private int find(int x) {
        if (fa[x] != x) {
            fa[x] = find(fa[x]);
        }
        return fa[x];
    }

    private void union(int x, int y) {
        fa[find(x)] = find(y);
    }

    public int[] findRedundantConnection(int[][] edges) {
        fa = new int[edges.length + 1];
        for (int i = 1; i <= edges.length; i++) {
            fa[i] = i;
        }
        for (int[] edge : edges) {
            if (find(edge[0]) == find(edge[1])) {
                return edge;
            } else {
                union(edge[0], edge[1]);
            }
        }
        return new int[0];
    }
}

Go

package main

func find(fa []int, x int) int {
    if fa[x] != x {
        fa[x] = find(fa, fa[x])
    }
    return fa[x]
}

func union(fa []int, x int, y int) {
    fa[find(fa, x)] = find(fa, y)
}

func findRedundantConnection(edges [][]int) []int {
    fa := make([]int, len(edges) + 1)
    for th, _ := range fa {
        fa[th] = th
    }
    for _, edge := range edges {
        if find(fa, edge[0]) == find(fa, edge[1]) {
            return edge
        } else {
            union(fa, edge[0], edge[1])
        }
    }
    return nil
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/143464726

今晚(20241102晚10:30)这会儿api.github.com似乎出了点问题，国内外都访问不到X_X