2476.二叉搜索树最近节点查询

【LetMeFly】2476.二叉搜索树最近节点查询：中序遍历 + 二分查找

力扣题目链接：https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的 二维 答案数组 answer ，其中 answer[i] = [mini, maxi] ：

• mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
• maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。

返回数组 answer 。

 

示例 1 ：

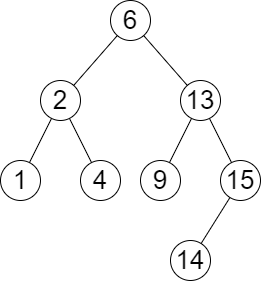
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2 ：

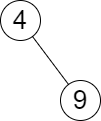
输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

 

提示：

• 树中节点的数目在范围 [2, 105] 内
• 1 <= Node.val <= 106
• n == queries.length
• 1 <= n <= 105
• 1 <= queries[i] <= 106

方法一：中序遍历 + 二分查找

首先要明确的是：

题目给的二叉搜索树不一定是平衡树。因此最坏的情况下，题目给的二叉搜索树可能会退化成一条链，单词搜索的时间复杂度可能会达到$O(n)$。

因为可能有很多次查询（$10^5$），所以我们可以预处理二叉搜索树：

我们知道二叉搜索树的中序遍历结果是递增的，因此我们中序遍历一遍二叉搜索树，就得到了二叉树所有节点值的递增数组。

这样，我们只需要遍历每一个查询，二分查找想要的答案即可：

对于查询$q$，使用内置函数lower_bound/bisect_left等找到第一个$\geq q$的位置$loc$。

判断$loc$是否超出数组范围：

• 若超出：说明无比$q$大的数，$M$应为（默认值）-1
• 否则：$M=v[loc]$。此时若$M$恰好等于$q$则可直接得到$m=M$

$m$仍未默认值-1的话，还要判断$loc$是否非零：

• 若非零：则$m=v[loc-1]$
• 否则：$m$为默认值-1

• 时间复杂度$O(N+Q\log N)$，其中$N$是二叉树节点个数，$Q$是查询个数
• 空间复杂度$O(N)$

AC代码

C++

class Solution {
private:
    vector<int> v;

    void dfs(TreeNode* root) {
        if (!root) {
            return;
        }
        dfs(root->left);
        v.push_back(root->val);
        dfs(root->right);
    }

public:
    vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {
        dfs(root);
        vector<vector<int>> ans(queries.size());
        for (int i = 0; i < queries.size(); i++) {
            int m = -1, M = -1;
            vector<int>::iterator it = lower_bound(v.begin(), v.end(), queries[i]);
            if (it != v.end()) {
                M = *it;
                if (M == queries[i]) {
                    m = M;
                    goto loop;
                }
            }
            if (it != v.begin()) {
                m = *(it - 1);
            }
            loop:
            ans[i] = {m, M};
        }
        return ans;
    }
};

Python

# from typing import List, Optional
# from bisect import bisect_left

# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def dfs(self, root: Optional[TreeNode]) -> None:
        if not root:
            return
        self.dfs(root.left)
        self.v.append(root.val)
        self.dfs(root.right)
    
    def closestNodes(self, root: TreeNode, queries: List[int]) -> List[List[int]]:
        self.v = []
        self.dfs(root)
        ans = []
        for q in queries:
            m, M = -1, -1
            loc = bisect_left(self.v, q)
            if loc != len(self.v):
                M = self.v[loc]  # v1中这里笔误写成M=loc了
                if M == q:
                    ans.append([q, q])
                    continue
            if loc:
                m = self.v[loc - 1]
            ans.append([m, M])
        return ans

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/136269516