1631.最小体力消耗路径

【LetMeFly】1631.最小体力消耗路径：广度优先搜索BFS

力扣题目链接：https://leetcode.cn/problems/path-with-minimum-effort/

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

 

示例 1：

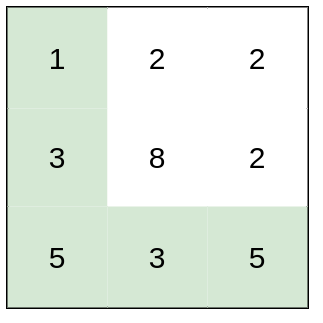
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

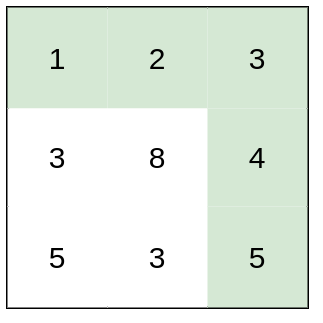
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

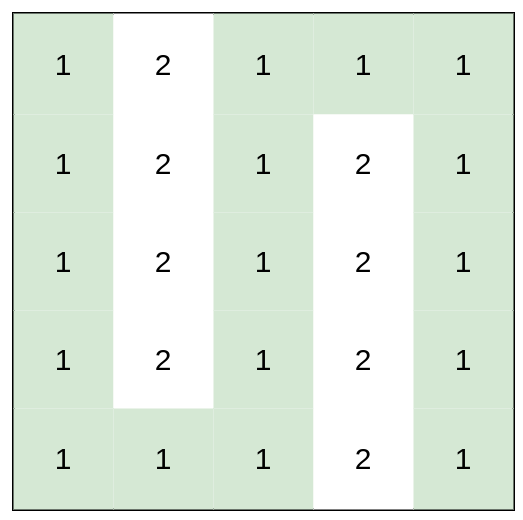
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

 

提示：

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

方法一：广度优先搜索BFS

首先我们可以构造一个图，图中顶点是矩阵中的点，图中的边是矩阵中相邻点的绝对值之差。

这样，我们只需要从起点0开始，使用一个优先队列进行广度优先搜索。每次找出未遍历的点中与已遍历的点中绝对值之差最小的点。入队时将“点的位置”和“从起点到该点的最大绝对值之差”入队。

最终返回最后一个位置距离起点的最大绝对值之差即为答案。

• 时间复杂度$O(nm\log nm)$，其中$size(graph)=n\times m$
• 空间复杂度$O(nm)$

AC代码

C++

const int directions[4][2] = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int n = heights.size(), m = heights[0].size();
        vector<vector<pair<int, int>>> graph(n * m);  // graph[i]: [[j, 5], [k, 3]]
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                for (int d = 0; d < 4; d++) {
                    int ti = i + directions[d][0], tj = j + directions[d][1];
                    if (ti < 0 || ti >= n || tj < 0 || tj >= m) {
                        continue;
                    }
                    int diff = abs(heights[i][j] - heights[ti][tj]);
                    int x = i * m + j, y = ti * m + tj;
                    graph[x].push_back({y, diff});
                }
            }
        }
        auto cmp = [](const pair<int, int>& a, const pair<int, int>& b) {
            return a.second > b.second;
        };
        priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
        pq.push({0, 0});
        vector<int> ans(n * m, 1e9);  // 从0到i的最大绝对值之差
        ans[0] = 0;
        while (pq.size()) {
            auto [index, diff] = pq.top();
            pq.pop();
            for (auto [toIndex, toDiff] : graph[index]) {
                int nextDiff = max(diff, toDiff);
                if (ans[toIndex] > nextDiff) {
                    ans[toIndex] = nextDiff;
                    pq.push({toIndex, nextDiff});
                }
            }
        }
        return ans.back();
    }
};

Python

# from typing import List
# import heapq


directions = [[-1, 0], [1, 0], [0, -1], [0, 1]]

class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        n, m = len(heights), len(heights[0])
        graph = [[] for _ in range(n * m)]
        for i in range(n):
            for j in range(m):
                for di, dj in directions:
                    ti, tj = i + di, j + dj
                    if ti < 0 or ti >= n or tj < 0 or tj >= m:
                        continue
                    graph[i * m + j].append((ti * m + tj, abs(heights[ti][tj] - heights[i][j])))
        pq = [(0, 0)]
        ans = [1000000000] * (n * m)
        ans[0] = 0
        while pq:
            thisDiff, thisNode = heapq.heappop(pq)
            for toNode, toDiff in graph[thisNode]:
                newDiff = max(thisDiff, toDiff)
                if ans[toNode] > newDiff:
                    ans[toNode] = newDiff
                    heapq.heappush(pq, (newDiff, toNode))
                    # print(thisNode, toNode, newDiff)
        return ans[-1]

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/134934684