1334.阈值距离内邻居最少的城市

【LetMeFly】1334.阈值距离内邻居最少的城市：多次运用单源最短路的迪杰斯特拉算法

力扣题目链接：https://leetcode.cn/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

 

示例 1：

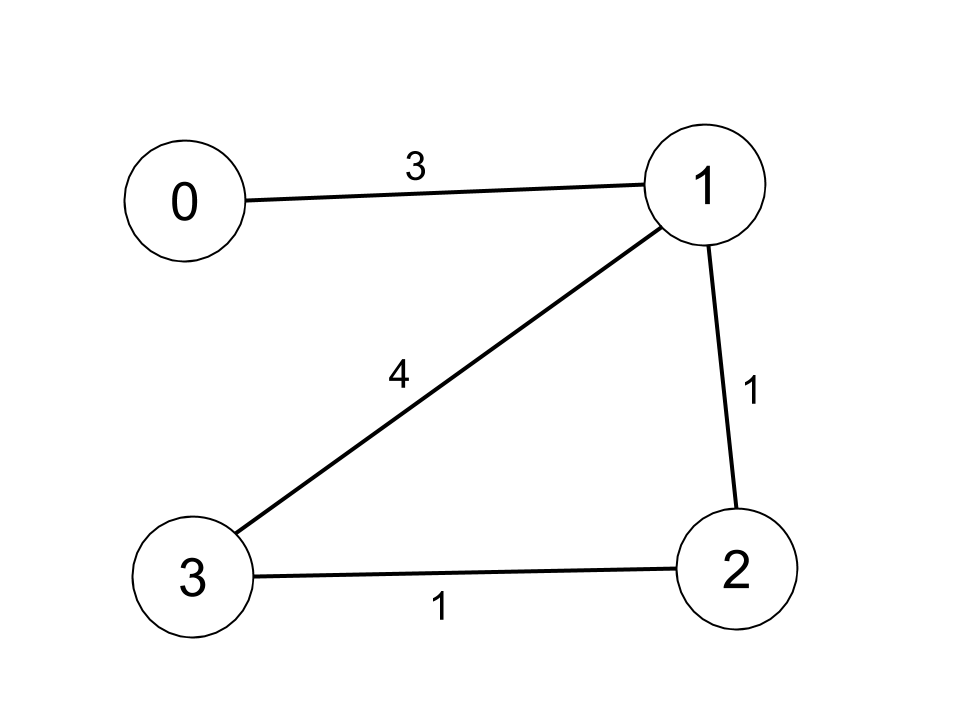
输入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出：3
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2] 
城市 1 -> [城市 0, 城市 2, 城市 3] 
城市 2 -> [城市 0, 城市 1, 城市 3] 
城市 3 -> [城市 1, 城市 2] 
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。

示例 2：

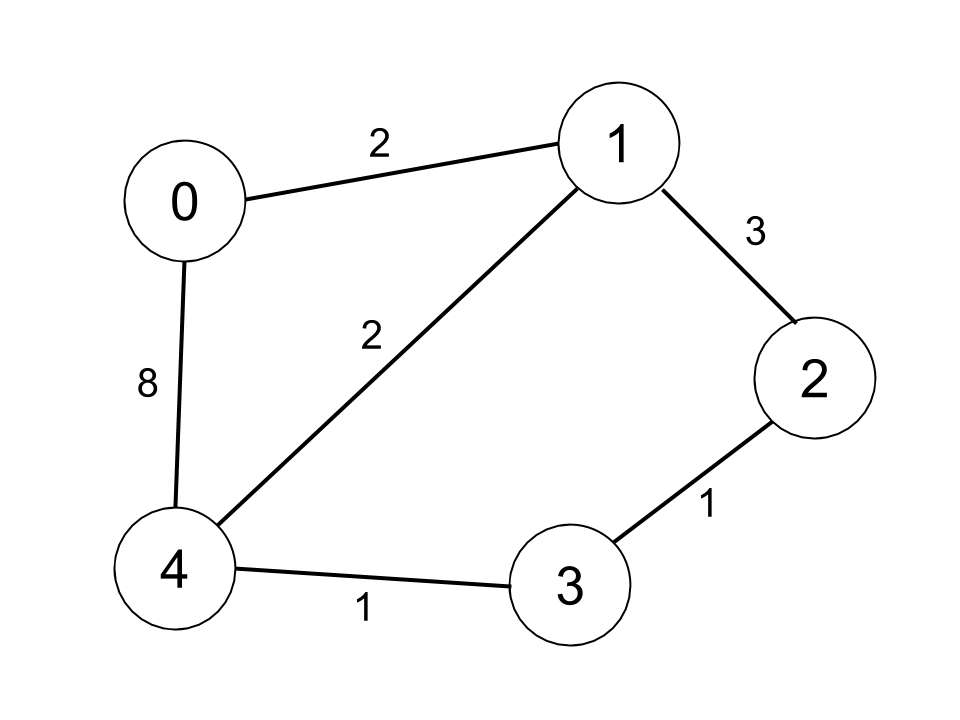
输入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出：0
解释：城市分布图如上。 
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1] 
城市 1 -> [城市 0, 城市 4] 
城市 2 -> [城市 3, 城市 4] 
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3] 
城市 0 在阈值距离 2 以内只有 1 个邻居城市。

 

提示：

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• 所有 (fromi, toi) 都是不同的。

方法一：多次运用单源最短路的迪杰斯特拉算法

迪杰斯特拉算法可以让我们在$O(n^2)$的时间复杂度内求出图中某点到其他所有点的最短路径。

关于单源最短路的迪杰斯特拉算法，推荐查看某人的视频讲解及配套代码。（算法本质是在所有能走的路中选一个最短的能到新节点的路来走）

这样，我们可以写一个函数来获取某个点不超过“distanceThreshold”的“邻居城市”的个数。

使用两个变量分别记录“最少的近邻个数”和“当前答案”，遍历一遍每个节点，计算并更新这两个变量即可得到答案。

• 时间复杂度$O(n^3)$
• 空间复杂度$O(size(graph) + n)$

AC代码

C++

class Solution {
private:
    int find1City(vector<vector<pair<int, int>>> &graph, int start, int Md) {
        vector<bool> visited(graph.size(), false);
        vector<int> minDistance(graph.size(), 1e9);
        minDistance[start] = 0;
        for (int i = 0; i < graph.size(); i++) {
            int thisMinDistance = 1e9;
            int thisShortestPoint = -1;
            for (int j = 0; j < graph.size(); j++) {
                if (!visited[j] && minDistance[j] < thisMinDistance) {
                    thisMinDistance = minDistance[j];
                    thisShortestPoint = j;
                }
            }
            if (thisMinDistance == 1e9) {
                break;
            }
            visited[thisShortestPoint] = true;
            for (auto& [toPoint, thisDistance] : graph[thisShortestPoint]) {
                if (minDistance[thisShortestPoint] + thisDistance < minDistance[toPoint]) {
                    minDistance[toPoint] = minDistance[thisShortestPoint] + thisDistance;
                }
            }
        }
        int ans = -1;
        for (int i = 0; i < graph.size(); i++) {
            if (minDistance[i] <= Md) {
                ans++;
            }
        }
        return ans;
    }
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        vector<vector<pair<int, int>>> graph(n);
        for (auto& v : edges) {
            graph[v[0]].push_back({v[1], v[2]});
            graph[v[1]].push_back({v[0], v[2]});
        }
        int mCan = n, Mnum = 0;
        for (int i = 0; i < n; i++) {
            int thisCity = find1City(graph, i, distanceThreshold);
            if (thisCity <= mCan) {
                mCan = thisCity;
                Mnum = i;
            }
        }
        return Mnum;
    }
};

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/134410277