1026.节点与其祖先之间的最大差值

【LetMeFly】1026.节点与其祖先之间的最大差值

力扣题目链接：https://leetcode.cn/problems/maximum-difference-between-node-and-ancestor/

给定二叉树的根节点 root，找出存在于 不同 节点 A 和 B 之间的最大值 V，其中 V = |A.val - B.val|，且 A 是 B 的祖先。

（如果 A 的任何子节点之一为 B，或者 A 的任何子节点是 B 的祖先，那么我们认为 A 是 B 的祖先）

 

示例 1：

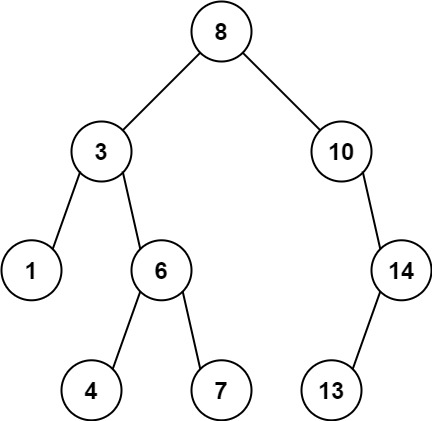
输入：root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出：7
解释： 
我们有大量的节点与其祖先的差值，其中一些如下：
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
在所有可能的差值中，最大值 7 由 |8 - 1| = 7 得出。

示例 2：

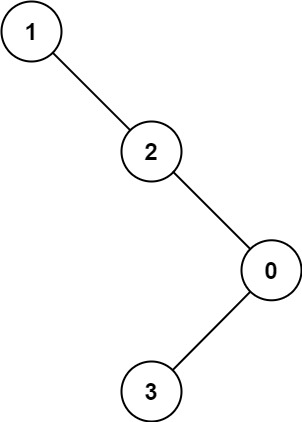
输入：root = [1,null,2,null,0,3]
输出：3

 

提示：

• 树中的节点数在 2 到 5000 之间。
• 0 <= Node.val <= 105

方法一：深度优先搜索DFS

有关深度优先搜索的题解有很多，本题也可以参考二叉树的前序遍历的深度优先搜索的方式进行求解。

在深度优先搜索的过程中，我们额外传递两个参数：分别是当前所有祖先节点的最大值 和 最小值。

这样，我们求出当前节点与最大值或最小值的绝对值之差，在所有节点的绝对值之差中，最大的那个即为答案。

• 时间复杂度$O(节点个数)$
• 空间复杂度$O(树的深度)$

AC代码

C++

class Solution {
private:
    int ans = 0;

    void dfs(TreeNode* root, int M, int m) {
        if (!root) {
            return;
        }
        ans = max(ans, abs(root->val - M));
        ans = max(ans, abs(root->val - m));
        M = max(M, root->val);
        m = min(m, root->val);
        dfs(root->left, M, m);
        dfs(root->right, M, m);
    }
public:
    int maxAncestorDiff(TreeNode* root) {
        dfs(root, root->val, root->val);
        return ans;
    }
};

Python

# from typing import Optional


# # Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right


class Solution:
    def __init__(self) -> None:
        self.ans = 0
    
    def dfs(self, root: Optional[TreeNode], M: int, m: int) -> None:
        if not root:
            return
        self.ans = max(self.ans, abs(root.val - M), abs(root.val - m))
        M = max(M, root.val)
        m = min(m, root.val)
        self.dfs(root.left, M, m)
        self.dfs(root.right, M, m)

    def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:
        self.dfs(root, root.val, root.val)
        return self.ans

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/130218910