1971.寻找图中是否存在路径

【LetMeFly】1971.寻找图中是否存在路径

力扣题目链接：https://leetcode.cn/problems/find-if-path-exists-in-graph/

有一个具有 n个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 start 开始，到顶点 end 结束的 有效路径 。

给你数组 edges 和整数 n、start和end，如果从 start 到 end 存在 有效路径 ，则返回 true，否则返回 false 。

 

示例 1：

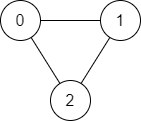
输入：n = 3, edges = [[0,1],[1,2],[2,0]], start = 0, end = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

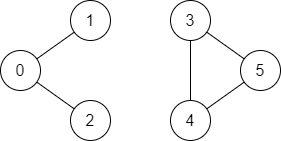
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], start = 0, end = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

 

提示:

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= start, end <= n - 1
• 不存在双向边
• 不存在指向顶点自身的边

方法一：广度优先搜索

首先我们把题目中给的图，以邻接表的形式存储下来（C++中可使用vector<vector>）

接着，再开辟一个大小未$n$的布尔类型的数组$visited$，其中$visited[n]$代表节点$n$是否被访问过，初始值全为$false$

然后建立一个队列，将起点入队。注意每入队一个节点，都需要将这个节点在$visited$中标记为$true$

当队列不为空时，将节点不断出队。对于出队的每个节点，遍历其相邻的所有节点。若有相邻节点未访问过，则入队。直到队列为空，我们就将与起点相联通的所有节点遍历完了。

最终$visited[destination]$即为答案

• 时间复杂度$O(n)$
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        vector<vector<int>> graph(n);
        for (auto& edge : edges) {
            graph[edge[0]].push_back(edge[1]);
            graph[edge[1]].push_back(edge[0]);
        }
        vector<bool> visited(n);
        visited[source] = true;
        queue<int> q;
        q.push(source);
        while (q.size()) {
            int thisNode = q.front();
            q.pop();
            for (int toNode : graph[thisNode]) {
                if (!visited[toNode]) {
                    visited[toNode] = true;
                    q.push(toNode);
                }
            }
        }
        return visited[destination];
    }
};

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/128377260