538.把二叉搜索树转换为累加树

【LetMeFly】538.把二叉搜索树转换为累加树

力扣题目链接：https://leetcode.cn/problems/convert-bst-to-greater-tree/

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

 

示例 1：

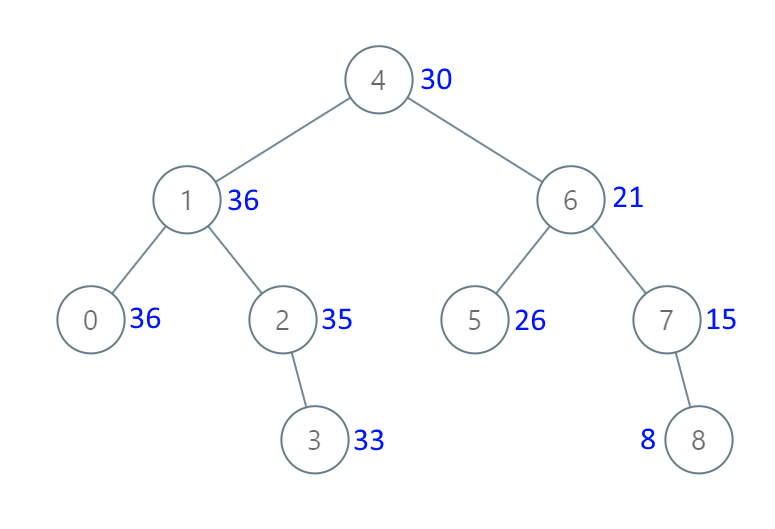
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

 

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

方法一：DFS反向中序遍历

二叉搜索树有一个非常不错的性质，就是“中序遍历所经过的节点的值是非递减的”。

同理，如果我们“反向中序遍历（右子->根->左子）”一颗二叉搜索树，那么我们的遍历顺序就是“非递增”的。

我们只需要记录一下“历史遍历节点的总和”，然后按照反向中序遍历的方式去遍历这棵二叉树，遍历到某个节点时，将这个节点的值修改为“这个节点的初始值 和 历史节点总和 的 和”，同时更新“历史遍历节点的总和”即可。

• 时间复杂度$O(n)$，其中$n$是二叉树节点的个数
• 空间复杂度$O(n)$

AC代码

C++

class Solution {
private:
    int total;

    void dfs(TreeNode* root) {
        if (!root)
            return;
        dfs(root->right);
        total = root->val = total + root->val;
        dfs(root->left);
    }
public:
    Solution() {total = 0;}

    TreeNode* convertBST(TreeNode* root) {
        dfs(root);
        return root;
    }
};

至于更高级的$O(1)$空间复杂度实现中序遍历的方法，请参考官方题解

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/128174296