1260.二维网格迁移

【LetMeFly】两种方法解决(k次模拟/一步到位)：1260.二维网格迁移

力扣题目链接：https://leetcode.cn/problems/shift-2d-grid/

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

• 位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
• 位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
• 位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

 

示例 1：

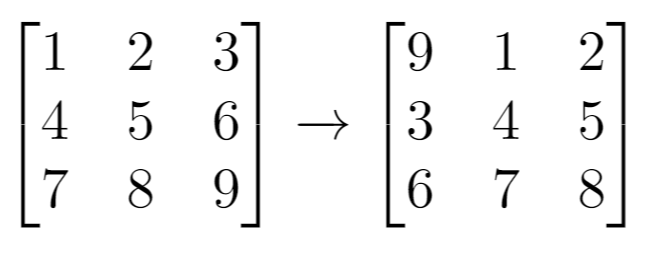
输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：

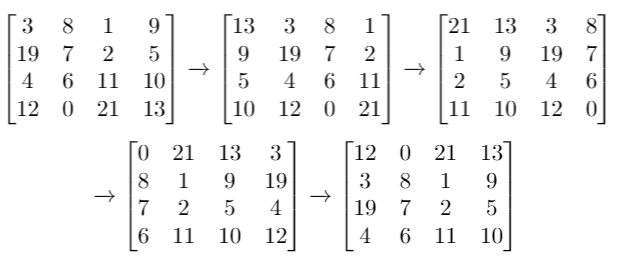
输入：grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

示例 3：

输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
输出：[[1,2,3],[4,5,6],[7,8,9]]

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

方法一：k次模拟

这种方法是一种彻彻底底的模拟方法

既然题目中说变换$k$次，那么就进行$k$次模拟。

每次模拟时，先记录下来最后一行的最后一个元素，然后从后往前依次赋值为上一个元素，最后再把第一个元素赋值为记录下来的元素即可。

这种方法的优点是可以原地修改数组，不需要很多的额外空间

• 时间复杂度$O(nmk)$，其中矩阵的大小为$n\times m$
• 空间复杂度$O(1)$，如果说答案不计入空间复杂度，那么与方法二相比，方法一的空间复杂度甚至为负数（没有这一说）

AC代码

C++

class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int n = grid.size(), m = grid[0].size();
        while (k--) {
            int last = grid[n - 1][m - 1];  // 先记下最后一行的最后一个元素
            for (int i = n - 1; i >= 0; i--) {
                for (int j = m - 1; j > 0; j--) {
                    grid[i][j] = grid[i][j - 1];  // 从后往前赋值为上一个元素
                }
				// 处理第i行的第一个元素
                if (i > 0)  // 如果不是第1行
                    grid[i][0] = grid[i - 1][m - 1];  // 就赋值为上一行的最后一个元素
                else  // 第1行
                    grid[i][0] = last;  // 赋值为先前记录下来的元素（最后一行最后一个）
            }
        }
        return grid;
    }
};

方法二：一步到位（降维打击）

这种方法是一种一步到位的方法

所谓一步到位，就是使用$O(1)$的时间，计算出当前位置的元素在经过$k$次变换后的位置。

具体怎么计算呢？

如果我们把二维数组降维打击至一维，就很容易理解了。

例如，我们把

1 2 3
4 5 6
7 8 9

转换成

1 2 3 4 5 6 7 8 9

那么，题目中所描述的变换，其实就是将一维数组中的每个元素循环右移$k$次。

在一位数组中，下标为$i$的元素，循环右移$k$次后的坐标为$(i+k) % mod$

剩下的问题就是二维坐标和一位坐标的转换。

二维坐标中的$(i,j)$等价于一位坐标中的$(i*m+j)$（根据变换规则即可得出），反之，一维坐标中的$th$等价于二维坐标中的$(th/m, th%m)$（向下取整）

那么问题就解决了。

这种方法的优点是时间复杂度低

• 时间复杂度$O(nm)$，其中矩阵的大小为$n\times m$
• 空间复杂度$O(1)$，和方法一相比，还是开辟了一个和原始矩阵等大小的空间。但是LeetCode的答案不计入空间复杂度，因此空间复杂度为$O(1)$

AC代码

C++

class Solution {
public:
    vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
        int n = grid.size(), m = grid[0].size();
        int size = n * m;
        vector<vector<int>> ans = grid;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int originalTh = i * m + j;
                int newTh = (originalTh + k) % size;
                ans[newTh / m][newTh % m] = grid[i][j];
            }
        }
        return ans;
    }
};

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/125889225