1367.二叉树中的链表

【LetMeFly】1367.二叉树中的链表：深度优先搜索(DFS) - 一步一步实现

力扣题目链接：https://leetcode.cn/problems/linked-list-in-binary-tree/

给你一棵以 root 为根的二叉树和一个 head 为第一个节点的链表。

如果在二叉树中，存在一条一直向下的路径，且每个点的数值恰好一一对应以 head 为首的链表中每个节点的值，那么请你返回 True ，否则返回 False 。

一直向下的路径的意思是：从树中某个节点开始，一直连续向下的路径。

 

示例 1：

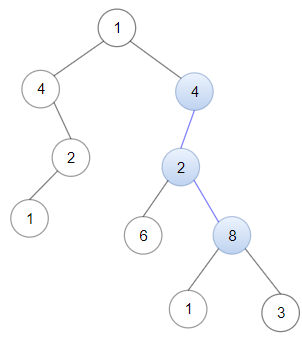
输入：head = [4,2,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true
解释：树中蓝色的节点构成了与链表对应的子路径。

示例 2：

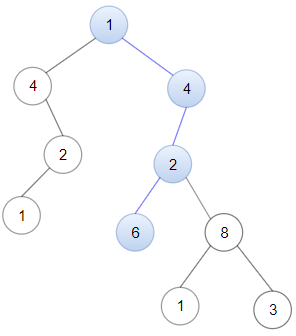
输入：head = [1,4,2,6], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：true

示例 3：

输入：head = [1,4,2,6,8], root = [1,4,4,null,2,2,null,1,null,6,8,null,null,null,null,1,3]
输出：false
解释：二叉树中不存在一一对应链表的路径。

 

提示：

• 二叉树和链表中的每个节点的值都满足 1 <= node.val <= 100 。
• 链表包含的节点数目在 1 到 100 之间。
• 二叉树包含的节点数目在 1 到 2500 之间。

解题方法：深度优先搜索DFS

如果我不匹配，只写一个深度优先搜索函数，怎么写？

void dfs(TreeNode* t) {
    if (!t) {
        return;
    }
    dfs(t->left);
    dfs(t->right);
}

现在还要加上匹配，所以要在dfs的同时返回匹配结果：

bool dfs(ListNode* l, TreeNode* t) {  // l是链表匹配到了哪个节点，t是二叉树匹配到了哪个节点
    // 这里写匹配判断
    ...
    if (dfs(head, t->left) || dfs(head, t->right)) {  // 前面没匹配成功，尝试递归时从子树开始重新匹配
        return true;
    }
    return false;  // 还是没有匹配成功
}

那么到底什么时候会匹配成功，什么时候匹配不成功呢？

1. 如果l为空，说明链表匹配完了，那不就是匹配成功了吗？返回true。
2. 如果t为空，说明二叉树匹配完了，匹配失败，返回false。
3. 如果l和t值相等，那是不是可以尝试匹配列表的下一个值和二叉树的下一个值了？开始递归匹配，若有匹配成功的情况则返回true。
4. 否则，递归子树节点，从链表头开始，尝试匹配。

bool dfs(ListNode* l, TreeNode* t) {
    if (!l) {
        return true;
    }
    if (!t) {
        return false;
    }
    if (l->val == t->val) {
        if (dfs(l->next, t->left) || dfs(l->next, t->right)) {
            return true;
        }
    }
    if (dfs(head, t->left) || dfs(head, t->right)) {  // 最后的匹配尝试
        return true;
    }
    return false;
}

这样真的可以了吗？仔细想想，在“最后的匹配尝试”这一步，我们使用t的左右子节点和链表的头节点重新进行匹配尝试。这会不会导致重复计算呢？

好像还真会，本来在最初版本递归的时候，就已经会有“二叉树每个节点和链表头节点开始匹配”这一项了。

如果二叉树节点和链表中间某节点匹配失败的时候，是不是就不应该再尝试“子节点从链表头开始匹配”了？

因此，在最后的“最后的匹配尝试”这一步之前应该加上一个特判：l == t。这样能保证只在“第一次递归”到时重投开始匹配。

bool dfs(ListNode* l, TreeNode* t) {
    if (!l) {
        return true;
    }
    if (!t) {
        return false;
    }
    if (l->val == t->val) {
        if (dfs(l->next, t->left) || dfs(l->next, t->right)) {
            return true;
        }
    }
    if (l == t) {  // 只在第一次递归到时匹配
        if (dfs(head, t->left) || dfs(head, t->right)) {  // 最后的匹配尝试
            return true;
        }
    }
    return false;
}

你也可以这么理解：

我可以写两个函数：深搜函数（只用来dfs二叉树，用二叉树的每个节点尝试和链表头节点开始匹配）、匹配函数（给定了二叉树节点和链表中的节点位置，只硬着头皮去匹配，失败了不再从头开始）

现在相当于我把两个函数合并为一个了，因此要判断是第一次递归到这个节点时从头开始匹配。

• 时间复杂度$O(mn)$，其中$m=size(ListNode), n=size(TreeNode)$
• 空间复杂度$O(n)$

AC代码

C++ - 人类友好版

/*
 * @Author: LetMeFly
 * @Date: 2024-12-30 14:08:08
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-30 14:11:54
 */
class Solution {
private:
    ListNode* head;

    bool dfs(ListNode* l, TreeNode* t) {
        if (!l) {
            return true;
        }
        if (!t) {
            return false;
        }
        if (l->val == t->val) {
            if (dfs(l->next, t->left) || dfs(l->next, t->right)) {
                return true;
            }
        }
        if (l == head) {
            if (dfs(l, t->left) || dfs(l, t->right)) {
                return true;
            }
        }
        return false;
    }
public:
    bool isSubPath(ListNode* head, TreeNode* root) {
        this->head = head;
        return dfs(head, root);
    }
};

C++ - 简写版

/*
 * @Author: LetMeFly
 * @Date: 2024-12-30 13:32:37
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2024-12-30 14:05:37
 */
class Solution {
private:
    bool dfs(ListNode* head, ListNode* l, TreeNode* t) {
        if (!l) {
            return true;
        }
        if (!t) {
            return false;
        }
        return l->val == t->val && (dfs(head, l->next, t->left) || dfs(head, l->next, t->right)) ||
               head == l && (dfs(head, l, t->left) || dfs(head, l, t->right));
    }
public:
    bool isSubPath(ListNode* head, TreeNode* root) {
        return dfs(head, head, root);
    }
};

Python

from typing import Optional

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def dfs(self, l: Optional[ListNode], r: Optional[TreeNode]) -> bool:
        if not l:
            return True
        if not r:
            return False
        if l.val == r.val:
            if self.dfs(l.next, r.left) or self.dfs(l.next, r.right):
                return True
        if l == self.head:
            if self.dfs(l, r.left) or self.dfs(l, r.right):
                return True
        return False

    def isSubPath(self, head: Optional[ListNode], root: Optional[TreeNode]) -> bool:
        self.head = head
        return self.dfs(head, root)

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

Tisfy：https://letmefly.blog.csdn.net/article/details/144826418